최장 증가 부분 수열(LIS, Longest Increasing Subsequence)란?
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 다음 조건을 만족하는 수열이다.
- 각 원소가 이전 원소보다 크다. (증가하고 있다)
- 그 길이가 최대이다
- 예를 들어, { 6, 2, 5, 1, 7, 4, 8, 3} 이라는 배열이 있을 경우, LIS는 { 2, 5, 7, 8 } 이다.
구현 방법
- DP를 이용한 방법
- 이분탐색을 이용한 방법
DP를 이용한 방법
알고리즘 설명
간단하지만 시간복잡도가 O(n^2)로 이분탐색보다는 큰 알고리즘이다
dp[i]: i번째 인덱스에서 끝나는 최장 증가 부분 수열의 길이
라고 한다면,
- 주어진 배열에서 인덱스를 한 칸씩(i+=1) 늘려가면서 확인합니다.
- 내부 반복문으로 i보다 작은 인덱스들을 하나씩 살펴(j+=1) 보면서 arr[j] < arr[i]인 것이 있을 경우
(내부 반복문 변수 j의 배열 값이 현재 인덱스 i 배열 값보다 작다면)
dp[i] = Math.max(dp[i], dp[j] + 1)로 업데이트한다.
- dp[i]: 기존의 dp[i]값
- dp[j]+1 : (내부 반복문 변수) j번째 인덱스에서 끝나는 최장 증가 부분 수열의 마지막에 arr[i]를 추가했을 때의 값 (+1)
이때 dp[i]값 중에서 가장 큰 값이 최장 증가 수열의 길이가 된다.
코드
public class LIS_DP {
public static void main(String[] args) {
int arr[] = {3, 2, 4, 1, 6};
int dp[] = new int[arr.length];
dp[0] = 1; // LIS의 첫 번째는 항상 1이다.
for (int i = 1; i < arr.length; i++) {
// 첫 원소부터 i원소 전까지 비교
for (int j = 0; j < i; j++) {
if (arr[j] < arr[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
// 증가 부분 수열의 길이는 1부터 시작하므로 0인 값을 1으로 변경해준다.
if (dp[i] == 0) {
dp[i] = 1;
}
}
}
System.out.println("arr : " + Arrays.toString(arr));
System.out.println("DP : " + Arrays.toString(dp));
}
}예시
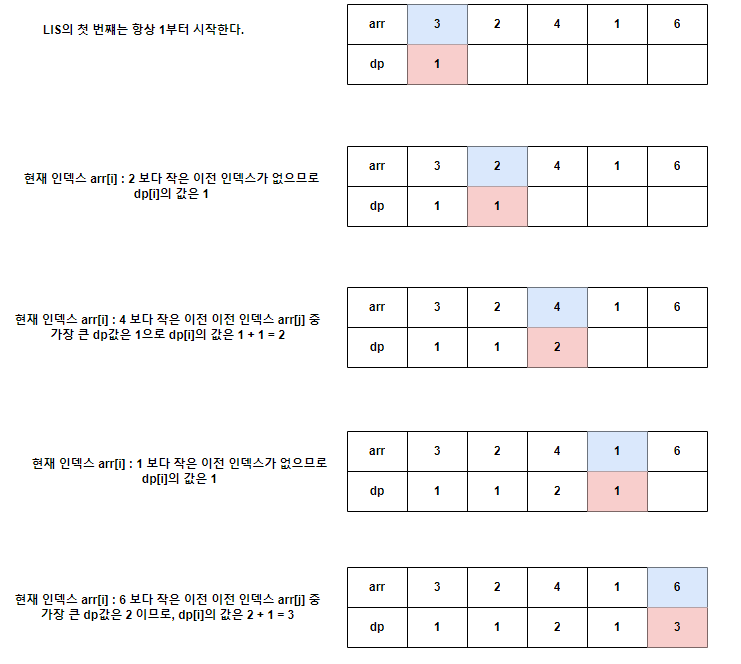
이분탐색을 이용한 방법
알고리즘 설명
DP보다는 복잡하지만 시간복잡도가 O(nlogn)으로 DP보다 효율적이다.
LIS의 형태를 유지하기 위해 주어진 배열의 인덱스를 하나씩 살펴보면서 그 숫자가 들어갈 위치를 이분탐색으로 탐색해서 넣는다.
이분 탐색을 활용할 때는 정확한 수열 값이 아닌 길이를 구해야 할 때 사용한다.
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[] memo;
static int INF = Integer.MIN_VALUE;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n];
StringTokenizer st= new StringTokenizer(br.readLine());
for(int i=0; i<n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
memo = new int[n+1];
int len=0;
int idx=0;
for(int i=0; i<n; i++) {
if(arr[i] > memo[len]) {
len +=1;
memo[len] = arr[i];
}else {
idx = binarySearch(0,len, arr[i]);
memo[idx] = arr[i];
}
}
System.out.println(len);
}
static int binarySearch(int left, int right, int key) {
int mid =0;
while(left<right) {
mid = (left+right)/2;
if(memo[mid] < key) {
left = mid+1;
}else {
right = mid;
}
}
return right;
}
}예시
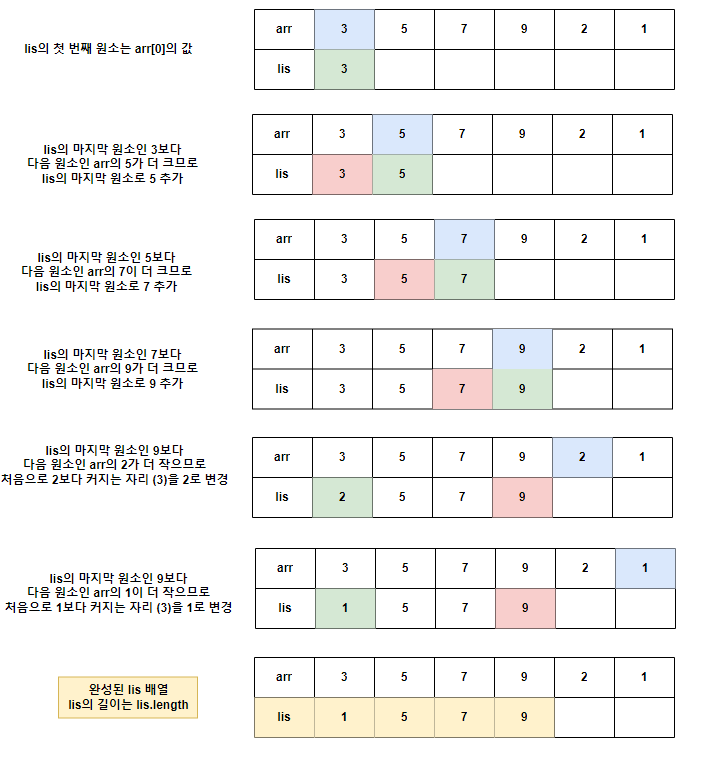
'CS > Algorithm' 카테고리의 다른 글
| Union-Find 연산에서 find함수 return할 때 주의할 점 (1) | 2024.07.24 |
|---|---|
| [그래프] 위상 정렬 (Topological Sorting) 알고리즘 (0) | 2024.07.23 |
| [MST] 프림 알고리즘 (Prim) (0) | 2024.07.22 |
| [MST] 크루스칼 알고리즘 (Kruskal) (0) | 2024.07.22 |
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
