프림 알고리즘이란?
트리 집합을 단계적으로 확장하는 것이다. 새로운 정점을 연결할 때마다 새로운 정점에서 갈 수 있는 아직 연결되지 않은 정점들에 대한 간선을 추가해줘야 한다.
이때 새로운 정점을 연결하는 것은 가중치를 기준으로 오름차순 정렬한 우선순위 큐에서 꺼낸다는 것이고, 단게적으로 확장하는 것은 이 우선순위 큐에서 뽑을 정점에서 연결 가능하고 방문하지 않은 정점을 우선순위 큐에 추가한다는 것이다.
배열로 구현할 경우 시간 복잡도 o(n^2)이고, 최소 힙으로 구현할 경우 시간 복잡도 O(Elog n)이다.
구현 방법
초기 상태로 정점(=노드)는 서로 연결되어 있지 않다. 정점과 연결된 간선을 하나씩 추가하면서 MST를 만든다. 우선 순위 큐에는 (정점, 가중치) 형식으로 저장되며, 첫 시작은 (시작 정점, 0)으로 넣는다. 우선 순위 큐가 빌 때까지 아래를 반복한다.
- 시작 정점을 정해 우선 순위 큐에 넣는다.
- 우선 순위 큐에서 하나를 꺼낸다.
- 꺼낸 정점 v를 방문했다면 2)로 돌아간다. 그렇지 않다면 아래를 진행한다.
- v와 연결된 간선을 모두 살핀다. 간선 (w, cost)는 v와 정점 w 사이 연결된 간선이며 cost 가중치를 가진다.
- 만약 w를 방문하지 않았다면 우선순위 큐에 추가한다.
예시
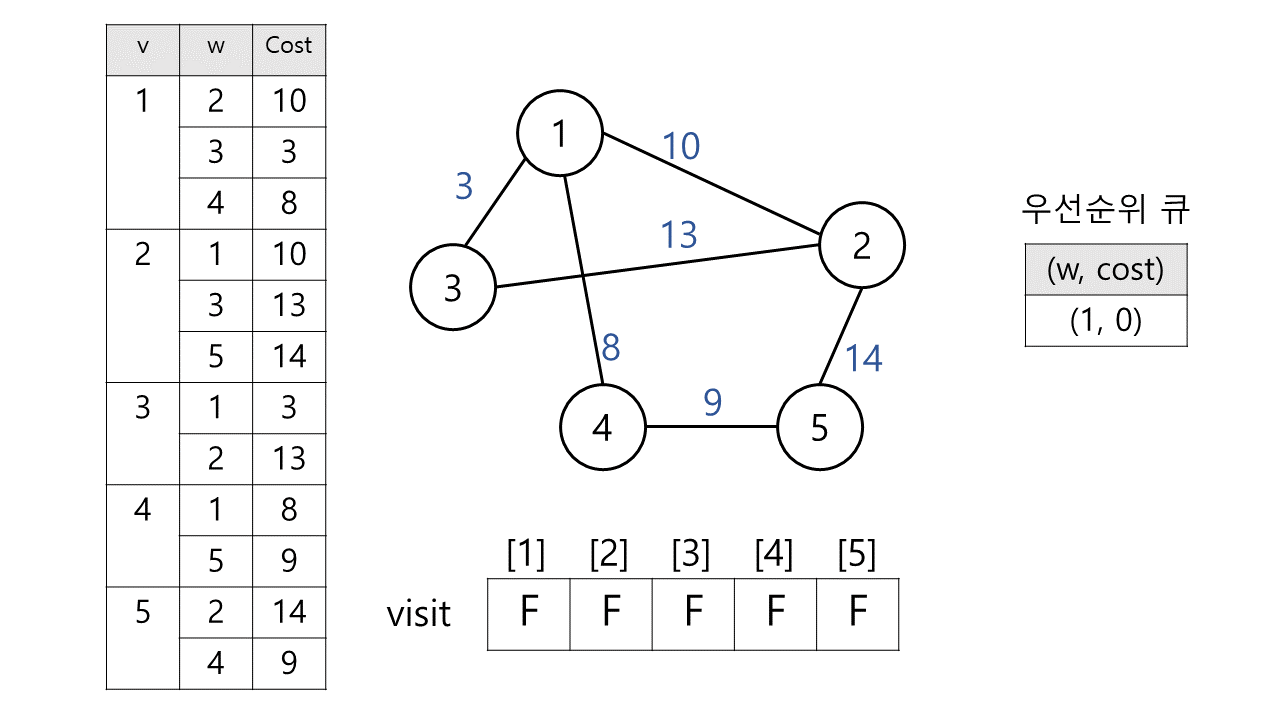
- 왼쪽 표 : 각 정점에 이어진 간선을 저장한 표이다.
- visit : boolean 배열로 각 정점을 방문했는지 체크한다.
정점을 방문 했다면 이미 MST에 포함된 정점이다. - 우선 순위 큐 : (정점, 가중치) 형태로 저장된다.
시작 정점은 1로 정했다. 따라서 우선 순위 큐에 (1, 0)를 저장했다.
1) 우선 순위 큐에서 하나 꺼낸다. → (1, 0)

정점 1은 아직 방문하지 않았으므로 방문 체크를 한다. 이제 정점 1은 MST에 속해있다.
이후 정점 1과 연결된 간선을 모두 살핀다.
- (3, 3) 우선 순위 큐에 추가
- (4, 8) 우선 순위 큐에 추가
- (2, 10) 우선 순위 큐에 추가
2) 우선 순위 큐에서 하나 꺼낸다. → (3, 3)

정점 3은 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 3과 가중치 3이 추가된다.
이후 정점 3과 연결된 간선을 모두 살핀다.
- (1, 3) 우선 순위 큐에 추가 X
정점 1은 이미 방문했다. 즉, 이미 MST에 포함된 정점이므로 우선 순위 큐에 추가하지 않는다. - (2, 13) 우선 순위 큐에 추가
3) 우선 순위 큐에서 하나 꺼낸다. → (4, 8)

정점 4은 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 4와 가중치 8이 추가된다.
이후 정점 4와 연결된 간선을 모두 살핀다
- (1, 8) 우선 순위 큐에 추가 X
- (5, 9) 우선 순위 큐에 추가
4) 우선 순위 큐에서 하나 꺼낸다. → (5, 9)

정점 5는 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 5와 가중치 9가 추가된다.
이후 정점 5와 연결된 간선을 모두 살핀다
- (2, 14) 우선 순위 큐에 추가
- (4, 9) 우선 순위 큐에 추가 X
5) 우선 순위 큐에서 하나 꺼낸다. → (2, 10)
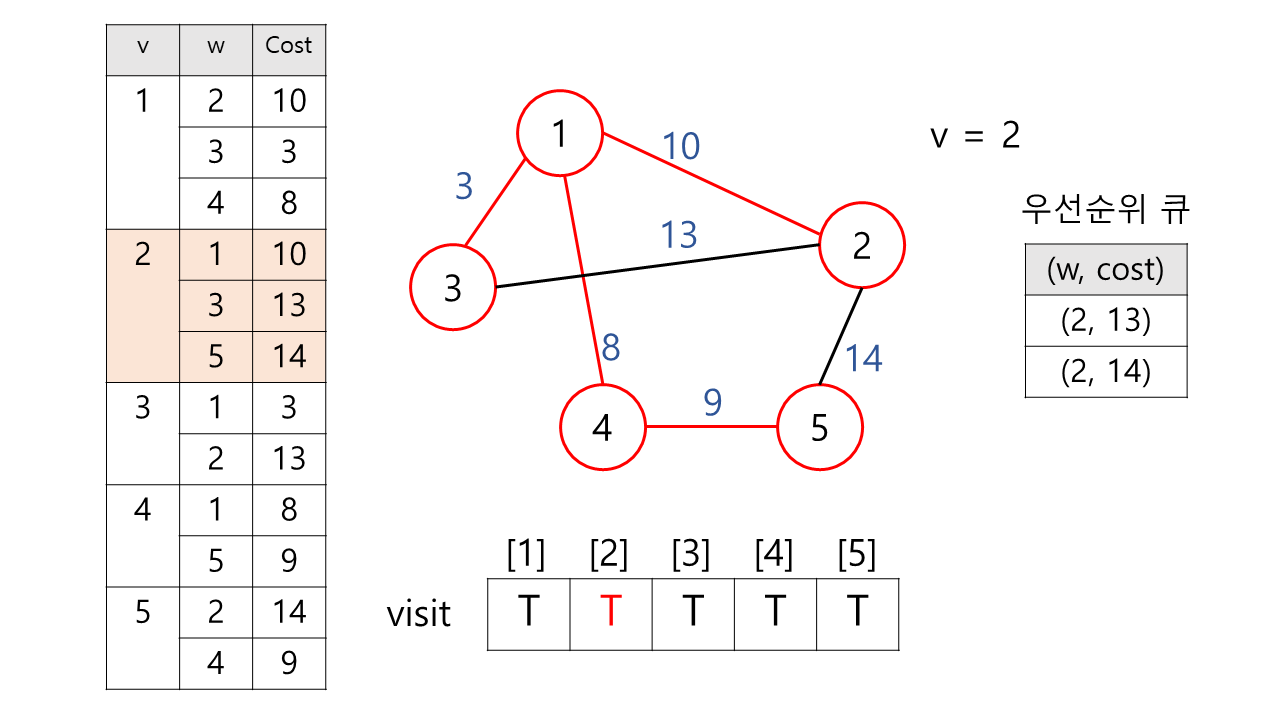
정점 2는 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 2와 가중치 10이 추가된다.
이후 정점 2와 연결된 간선을 모두 살핀다
- (1, 10) 우선 순위 큐에 추가 X
- (3, 13) 우선 순위 큐에 추가 X
- (5, 14) 우선 순위 큐에 추가 X
연결된 간선 모두 이미 MST에 포함된 정점과 연결되어 있으므로 우선 순위 큐에 포함하지 않는다.
6) 우선 순위 큐에서 하나 꺼낸다. → (2, 13)

정점 2는 이미 방문했다. 즉, 이미 MST에 포함된 상태이므로 건너뛴다.
7) 우선 순위 큐에서 하나 꺼낸다. -> (2, 14)

위와 동일한 이유로 건너뛴다.
우선 순위 큐가 비었으므로 MST가 완성되었다. 아래는 최종 MST의 모습이며 총 가중치는 30이다.

코드
// 간선 저장 위한 클래스
class Edge implements Comparable<Edge>{
int w; // 간선 들어오는 정점
int cost; // 간선 가중치
Edge(int w, int cost){
this.w = w;
this.cost = cost;
}
// 간선 오름차순으로 정렬
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
// 프림 알고리즘
public static void prim(int start, int n) {
boolean[] visit = new boolean[n + 1];
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(start, 0));
int total = 0;
while(!pq.isEmpty()) {
Edge edge = pq.poll();
int v = edge.w;
int cost = edge.cost;
//방문 했으면 건너뜀
if(visit[v]) continue;
visit[v] = true;
total += cost;
for(Edge e : graph[v]) {
if(!visit[e.w]) {
pq.add(e);
}
}
}
// 완성된 최소 신장 트리의 총 가중치 합 출력
System.out.println(total);
}
예시 문제: https://www.acmicpc.net/problem/21924
- 양 방향인 것에 주의
- return 타입 long 주의
- 방문하지 않으면 -1 출력해야 함
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class _21924 {
static int v;
static boolean[] visited;
public static void main(String[] args)throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
v=Integer.parseInt(st.nextToken());
int e=Integer.parseInt(st.nextToken());
ArrayList<Node>[] nodes=new ArrayList[v+1];
for(int i=0;i<=v;i++){
nodes[i]=new ArrayList<>();
}
long sum=0;
for(int i=0;i<e;i++){
st=new StringTokenizer(br.readLine());
int start=Integer.parseInt(st.nextToken());
int end=Integer.parseInt(st.nextToken());
int value=Integer.parseInt(st.nextToken());
sum+=value;
nodes[start].add(new Node(end,value));
nodes[end].add(new Node(start,value));
}
long cost=prim(nodes,1);
boolean allVisited = true;
for (int i = 1; i <= v; i++) {
if (!visited[i]) {
allVisited = false;
break;
}
}
if (!allVisited) {
System.out.println(-1);
} else {
System.out.println(sum - cost);
}
}
public static long prim(ArrayList<Node>[] nodes, int start){
visited=new boolean[v+1];
PriorityQueue<Node> que=new PriorityQueue<>((o1, o2) -> o1.value-o2.value);
que.add(new Node(start,0));
long cost=0;
while(!que.isEmpty()){
Node cur=que.poll();
if(visited[cur.idx])
continue;
visited[cur.idx]=true;
cost+=cur.value;
for(Node n:nodes[cur.idx]){
if(!visited[n.idx]){
que.add(new Node(n.idx,n.value));
}
}
}
return cost;
}
public static class Node{
public int idx;
public int value;
public Node(int idx, int value){
this.idx=idx;
this.value=value;
}
}
}'CS > Algorithm' 카테고리의 다른 글
| Union-Find 연산에서 find함수 return할 때 주의할 점 (1) | 2024.07.24 |
|---|---|
| [그래프] 위상 정렬 (Topological Sorting) 알고리즘 (0) | 2024.07.23 |
| [MST] 크루스칼 알고리즘 (Kruskal) (0) | 2024.07.22 |
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
| [최단거리] 플로이드-워셜 알고리즘 (Floyd-Warshal) (0) | 2024.07.11 |
