위상정렬 알고리즘이란?
정렬 알고리즘의 일종으로, 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 이때 위상정렬은 사이클이 없는 방향 그래프(DAG)에서만 가능하다. 인접 리스트를 사용하면 시간 복잡도가 O(V+E)이고 인접 행렬을 사용하면 시간 복잡도가 O(V^2)이다.

위 DAG 그래프를 위상정렬하면 아래와 같이 여러 결과가 나올 수 있다.

구현 방법
진입차수를 이용한 BFS 방법과 재귀를 이용한 DFS 방법이 있다.
BFS 방법
알고리즘 설명
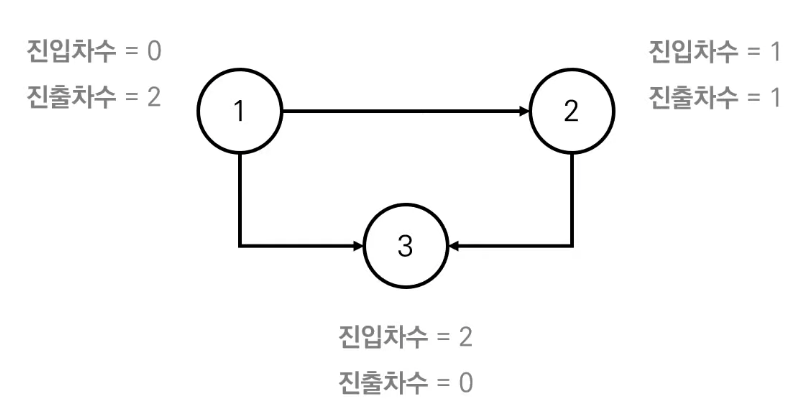
- 진입차수 (in-degree) : 특정한 노드로 들어오는 간선의 개수
- 진출차수 (out-degree) : 특정한 노드에서 나가는 간선의 개수
- (시작) 진입차수가 0인 정점을 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 T(위상 정렬 순서를 나타내는 리스트)에 추가한다.
- 해당 노드에서 인접한 정점중 정점의 in_degree 0보다 크면
- in_degree 1 감소한다.
- 위에서 in_degree가 1 감소한 결과가 0이 되면 큐에 추가한다.
- 해당 노드에서 인접한 정점중 정점의 in_degree 0보다 크면
- 큐에서 원소를 꺼내 T(위상 정렬 순서를 나타내는 리스트)에 추가한다.
예시

1) 초기화

모든 정점의in_degree를 설정한다.
2) in_dgree 0인 정점 방문

in_degree가 0인 정점 3을 큐에 삽입하고 방문표시
3) 정점 3의 인접한 정점 0, 4 방문

- 정점 3을 T에 추가
- 정점 3에 인접한 정점중 방문하지 않은 정점 (0, 4)의 in_degree의 값 감소
- in_degree 값이 0이 된 정점 0, 4를 queue에 추가하고 방문 표시
4) 정점 0의 인접한 정점 1 방문

- 큐에서 정점 0을 T에 추가
- 정점 0에 인접한 정점중 방문하지 않은 정점 1의 in_degree를 감소.
5) 정점 4의 인접한 정점 1,2 방문

- 큐에서 정점 4를 T에 추가
- 정점 4에 인접한 정점중 방문하지 않은 정점 1, 2의 in_degree를 감소
- in_degree값이 0인 정점 1을 큐에 추가하고 방문 표시
Step 6.

- 큐에서 정점 1을 T에 추가
- 정점 1에 인접한 정점중 방문하지 않은 정점 2의 in_degree를 감소
- in_degree값이 0인 정점 2를 큐에 추가하고 방문 표시
Step 7.

- 큐에서 정점 2를 가져와 T에 추가
- 정점 2에 인접한 정점중 방문하지 않은 정점 5의 in-dgree를 감소
- in_degree값이 0인 정점 5를 큐에 넣고 방문 표시
Step 8.

- 큐에서 정점 5를 가져와 T에 추가
- 더 이상 큐에 정점이 없으므로 종료
코드
import java.util.*;
class Graph {
private int vertexNumber;
private List<List<Integer>> adj;
private int[] inDegree;
private boolean[] visited;
public Graph(int vertexNumber) {
this.vertexNumber = vertexNumber;
adj = new ArrayList<>();
for (int i = 0; i < vertexNumber; i++) {
adj.add(new LinkedList<>());
}
inDegree = new int[vertexNumber];
visited = new boolean[vertexNumber];
}
public void addEdge(int src, int dest) {
adj.get(src).add(dest);
inDegree[dest]++;
}
}
class TopologicalSort {
public void topologicalSort(Graph graph) {
Queue<Integer> queue = new LinkedList<>();
List<Integer> topOrder = new ArrayList<>();
for (int i = 0; i < graph.inDegree.length; i++) {
if (graph.inDegree[i] == 0 && !graph.visited[i]) {
queue.add(i);
graph.visited[i] = true;
}
}
while (!queue.isEmpty()) {
int vertex = queue.poll();
topOrder.add(vertex);
for (int adjVertex : graph.adj.get(vertex)) {
if (!graph.visited[adjVertex] && --graph.inDegree[adjVertex] == 0) {
queue.add(adjVertex);
graph.visited[adjVertex] = true;
}
}
}
for (int vertex : topOrder) {
System.out.print(vertex + " ");
}
}
public static void main(String[] args) {
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
TopologicalSort tSort = new TopologicalSort();
tSort.topologicalSort(g);
}
}DFS 방법
알고리즘 설명
- 하나의 정점에서 시작
- 방문표시를 하면서 간선을 따라 다음 정점으로 방문
- 더 이상 방문할 간선이 없으면 리스트 앞에 정점을 추가하고 backtracking을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인
- 방문 가능한 간선이 있다면 다시 간선을 따라 다음 정점으로 이동합니다.
- 모든 정점을 탐색할 때까지 2-4단계 반복
예시


1) 정점 0에서 시작해 Stack T에 추가한다.
2) 정점 0이 가리키는 정점인 1을 Stack에 추가한다. (방문 표시)
3) 정점 1이 가리키는 정점인 2를 Stack에 추가한다. (방문 표시)
4) 정점 2가 가리키는 정점인 5를 Stack에 추가한다. (방문 표시)
5) 정점 5는 가리키는 정점이 없으므로 Stack에서 pop해주고 T에 추가한다.
6) 정점 2가 가리키는 정점 중 방문하지 않은 정점이 없으므로 pop해주고 T에 offerFirst(2)를 한다.
7) 정점 1이 가리키는 정점 중 방문하지 않은 정점이 없으므로 pop해주고 T에 offerFirst(1)를 한다.
8) 정점 0이 가리키는 정점 중 방문하지 않은 정점이 없으므르 pop해주고 T에 offerFirst(0)을 한다.
9) Stack이 비어있으므로 방문하지 않은 정점 중 아무 점인 3을 방문하고, Stack에 추가한다.
10) 정점 3이 가리키는 정점인 4를 Stack에 추가한다. (방문 표시)
11) 정점 4가 가리키는 정점 중 방문하지 않은 정점이 없으므로 Stack에서 pop해주고 T에 offerFirst(4)를 한다.
12) 정점 3이 가리키는 정점 중 방문하지 않은 정점이 없으므로 Stack에서 pop해주고 T에 offerFirst(3)를 한다.
코드
import java.util.*;
class Graph {
private int vertexNumber;
private List<List<Integer>> adj;
private boolean[] visited;
public Graph(int vertexNumber) {
this.vertexNumber = vertexNumber;
adj = new ArrayList<>();
for (int i = 0; i < vertexNumber; i++) {
adj.add(new LinkedList<>());
}
visited = new boolean[vertexNumber];
}
public void addEdge(int src, int dest) {
adj.get(src).add(dest);
}
public List<Integer> getAdj(int vertex) {
return adj.get(vertex);
}
public boolean isVisited(int vertex) {
return visited[vertex];
}
public void setVisited(int vertex, boolean value) {
visited[vertex] = value;
}
public int getVertexNumber() {
return vertexNumber;
}
}
public class TopologicalSortDFS {
private Stack<Integer> stack;
public TopologicalSortDFS() {
stack = new Stack<>();
}
public void topologicalSort(Graph graph) {
for (int i = 0; i < graph.getVertexNumber(); i++) {
if (!graph.isVisited(i)) {
dfs(graph, i);
}
}
while (!stack.isEmpty()) {
System.out.print(stack.pop() + " ");
}
}
private void dfs(Graph graph, int v) {
graph.setVisited(v, true);
for (int adjVertex : graph.getAdj(v)) {
if (!graph.isVisited(adjVertex)) {
dfs(graph, adjVertex);
}
}
stack.push(v);
}
public static void main(String[] args) {
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
TopologicalSortDFS sortDFS = new TopologicalSortDFS();
sortDFS.topologicalSort(g);
}
}참고
위상 정렬(Topological sort) 개념 및 구현
목차 위상 정렬(Topological sort) 개념 및 구현 비순환 방향 그래프 (DAG: Directed Acyclic Graph) Directed Acyclic Graph (DAG)는 사이클이 없는 방향 그래프입니다. DAG는 이벤트 간의 우선순위를 나타내기 위해 주
yoongrammer.tistory.com
예시 문제: https://www.acmicpc.net/problem/1005
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Queue;
import java.util.StringTokenizer;
public class _1005 {
public static boolean[] visited;
public static int N;
public static int sum;
public static int total;
public static int[] buildTime;
public static ArrayList<Integer>[] graph;
public static int[] in_degree;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); //건물 개수
int K = Integer.parseInt(st.nextToken()); //규칙 개수
buildTime = new int[N + 1];//건물 짓느데 걸리는 시간
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
buildTime[j] = Integer.parseInt(st.nextToken());
}
graph = new ArrayList[N + 1];
for (int k = 0; k <= N; k++) {
graph[k] = new ArrayList<>();
}
for (int k = 0; k < K; k++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph[start].add(end);
}
in_degree = new int[N + 1];
for (int j = 0; j <= N; j++) {
if (!graph[j].isEmpty()) {
for (int k : graph[j]) {
in_degree[k]++;
}
}
}
int obj = Integer.parseInt(br.readLine());
System.out.println(topoSort(obj));
}
}
public static int topoSort(int obj) {
int[] time = new int[N + 1];
Queue<Integer> curIdx = new ArrayDeque<>();
for (int i = 1; i <= N; i++) {
time[i] = buildTime[i];
if (in_degree[i] == 0) {
curIdx.add(i);
}
}
while (!curIdx.isEmpty()) {
int idx = curIdx.poll();
for (int i : graph[idx]) {
time[i] = Math.max(time[i], time[idx] + buildTime[i]);
in_degree[i]--;
if(in_degree[i]==0)
curIdx.add(i);
}
}
return time[obj];
}
}예시 문제: https://www.acmicpc.net/problem/14567
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class _14567 {
public static void main(String[] args)throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
int N=Integer.parseInt(st.nextToken());
int M=Integer.parseInt(st.nextToken());
int[] in_degree=new int[N+1];
Arrays.fill(in_degree, 1);
ArrayList<Integer>[] graph=new ArrayList[N+1];
for(int i=0;i<=N;i++){
graph[i]=new ArrayList<>();
}
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine());
int start=Integer.parseInt(st.nextToken());
int end=Integer.parseInt(st.nextToken());
graph[start].add(end);
}
for(int i=1;i<=N;i++){
if(!graph[i].isEmpty()){
for(int j:graph[i]){
in_degree[j]=Math.max(in_degree[j], in_degree[i]+1);
}
}
}
for(int i=1;i<=N;i++){
System.out.print(in_degree[i]+" ");
}
}
}예시 문제: https://www.acmicpc.net/problem/1766
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class _1766 {
static ArrayList<Integer>[] graph;
static ArrayList<Integer> answer;
static int[] in_degree;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
in_degree = new int[N + 1];
graph = new ArrayList[N + 1];
for (int i = 0; i <= N; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
in_degree[end] += 1;
graph[start].add(end);
}
for (int i = 0; i <= N; i++) {
Collections.sort(graph[i]);
}
answer = new ArrayList<>();
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 1; i <= N; i++) {
if(in_degree[i]==0)
pq.add(i);
}
while(!pq.isEmpty()){
Integer idx=pq.poll();
answer.add(idx);
for(int next:graph[idx]){
if(--in_degree[next]==0){
pq.add(next);
}
}
}
for(int i:answer){
System.out.print(i+" ");
}
}
}'CS > Algorithm' 카테고리의 다른 글
| [LIS] 최장 증가 부분 수열 (0) | 2024.08.01 |
|---|---|
| Union-Find 연산에서 find함수 return할 때 주의할 점 (1) | 2024.07.24 |
| [MST] 프림 알고리즘 (Prim) (0) | 2024.07.22 |
| [MST] 크루스칼 알고리즘 (Kruskal) (0) | 2024.07.22 |
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
위상정렬 알고리즘이란?
정렬 알고리즘의 일종으로, 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 이때 위상정렬은 사이클이 없는 방향 그래프(DAG)에서만 가능하다. 인접 리스트를 사용하면 시간 복잡도가 O(V+E)이고 인접 행렬을 사용하면 시간 복잡도가 O(V^2)이다.

위 DAG 그래프를 위상정렬하면 아래와 같이 여러 결과가 나올 수 있다.

구현 방법
진입차수를 이용한 BFS 방법과 재귀를 이용한 DFS 방법이 있다.
BFS 방법
알고리즘 설명
- 진입차수 (in-degree) : 특정한 노드로 들어오는 간선의 개수
- 진출차수 (out-degree) : 특정한 노드에서 나가는 간선의 개수

- (시작) 진입차수가 0인 정점을 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 T(위상 정렬 순서를 나타내는 리스트)에 추가한다.
- 해당 노드에서 인접한 정점중 정점의 in_degree 0보다 크면
- in_degree 1 감소한다.
- 위에서 in_degree가 1 감소한 결과가 0이 되면 큐에 추가한다.
- 해당 노드에서 인접한 정점중 정점의 in_degree 0보다 크면
- 큐에서 원소를 꺼내 T(위상 정렬 순서를 나타내는 리스트)에 추가한다.
예시

1) 초기화

모든 정점의in_degree를 설정한다.
2) in_dgree 0인 정점 방문

in_degree가 0인 정점 3을 큐에 삽입하고 방문표시
3) 정점 3의 인접한 정점 0, 4 방문

- 정점 3을 T에 추가
- 정점 3에 인접한 정점중 방문하지 않은 정점 (0, 4)의 in_degree의 값 감소
- in_degree 값이 0이 된 정점 0, 4를 queue에 추가하고 방문 표시
4) 정점 0의 인접한 정점 1 방문

- 큐에서 정점 0을 T에 추가
- 정점 0에 인접한 정점중 방문하지 않은 정점 1의 in_degree를 감소.
5) 정점 4의 인접한 정점 1,2 방문

- 큐에서 정점 4를 T에 추가
- 정점 4에 인접한 정점중 방문하지 않은 정점 1, 2의 in_degree를 감소
- in_degree값이 0인 정점 1을 큐에 추가하고 방문 표시
Step 6.

- 큐에서 정점 1을 T에 추가
- 정점 1에 인접한 정점중 방문하지 않은 정점 2의 in_degree를 감소
- in_degree값이 0인 정점 2를 큐에 추가하고 방문 표시
Step 7.

- 큐에서 정점 2를 가져와 T에 추가
- 정점 2에 인접한 정점중 방문하지 않은 정점 5의 in-dgree를 감소
- in_degree값이 0인 정점 5를 큐에 넣고 방문 표시
Step 8.

- 큐에서 정점 5를 가져와 T에 추가
- 더 이상 큐에 정점이 없으므로 종료
코드
import java.util.*; class Graph { private int vertexNumber; private List<List<Integer>> adj; private int[] inDegree; private boolean[] visited; public Graph(int vertexNumber) { this.vertexNumber = vertexNumber; adj = new ArrayList<>(); for (int i = 0; i < vertexNumber; i++) { adj.add(new LinkedList<>()); } inDegree = new int[vertexNumber]; visited = new boolean[vertexNumber]; } public void addEdge(int src, int dest) { adj.get(src).add(dest); inDegree[dest]++; } } class TopologicalSort { public void topologicalSort(Graph graph) { Queue<Integer> queue = new LinkedList<>(); List<Integer> topOrder = new ArrayList<>(); for (int i = 0; i < graph.inDegree.length; i++) { if (graph.inDegree[i] == 0 && !graph.visited[i]) { queue.add(i); graph.visited[i] = true; } } while (!queue.isEmpty()) { int vertex = queue.poll(); topOrder.add(vertex); for (int adjVertex : graph.adj.get(vertex)) { if (!graph.visited[adjVertex] && --graph.inDegree[adjVertex] == 0) { queue.add(adjVertex); graph.visited[adjVertex] = true; } } } for (int vertex : topOrder) { System.out.print(vertex + " "); } } public static void main(String[] args) { Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); TopologicalSort tSort = new TopologicalSort(); tSort.topologicalSort(g); } }
DFS 방법
알고리즘 설명
- 하나의 정점에서 시작
- 방문표시를 하면서 간선을 따라 다음 정점으로 방문
- 더 이상 방문할 간선이 없으면 리스트 앞에 정점을 추가하고 backtracking을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인
- 방문 가능한 간선이 있다면 다시 간선을 따라 다음 정점으로 이동합니다.
- 모든 정점을 탐색할 때까지 2-4단계 반복
예시


1) 정점 0에서 시작해 Stack T에 추가한다.
2) 정점 0이 가리키는 정점인 1을 Stack에 추가한다. (방문 표시)
3) 정점 1이 가리키는 정점인 2를 Stack에 추가한다. (방문 표시)
4) 정점 2가 가리키는 정점인 5를 Stack에 추가한다. (방문 표시)
5) 정점 5는 가리키는 정점이 없으므로 Stack에서 pop해주고 T에 추가한다.
6) 정점 2가 가리키는 정점 중 방문하지 않은 정점이 없으므로 pop해주고 T에 offerFirst(2)를 한다.
7) 정점 1이 가리키는 정점 중 방문하지 않은 정점이 없으므로 pop해주고 T에 offerFirst(1)를 한다.
8) 정점 0이 가리키는 정점 중 방문하지 않은 정점이 없으므르 pop해주고 T에 offerFirst(0)을 한다.
9) Stack이 비어있으므로 방문하지 않은 정점 중 아무 점인 3을 방문하고, Stack에 추가한다.
10) 정점 3이 가리키는 정점인 4를 Stack에 추가한다. (방문 표시)
11) 정점 4가 가리키는 정점 중 방문하지 않은 정점이 없으므로 Stack에서 pop해주고 T에 offerFirst(4)를 한다.
12) 정점 3이 가리키는 정점 중 방문하지 않은 정점이 없으므로 Stack에서 pop해주고 T에 offerFirst(3)를 한다.
코드
import java.util.*; class Graph { private int vertexNumber; private List<List<Integer>> adj; private boolean[] visited; public Graph(int vertexNumber) { this.vertexNumber = vertexNumber; adj = new ArrayList<>(); for (int i = 0; i < vertexNumber; i++) { adj.add(new LinkedList<>()); } visited = new boolean[vertexNumber]; } public void addEdge(int src, int dest) { adj.get(src).add(dest); } public List<Integer> getAdj(int vertex) { return adj.get(vertex); } public boolean isVisited(int vertex) { return visited[vertex]; } public void setVisited(int vertex, boolean value) { visited[vertex] = value; } public int getVertexNumber() { return vertexNumber; } } public class TopologicalSortDFS { private Stack<Integer> stack; public TopologicalSortDFS() { stack = new Stack<>(); } public void topologicalSort(Graph graph) { for (int i = 0; i < graph.getVertexNumber(); i++) { if (!graph.isVisited(i)) { dfs(graph, i); } } while (!stack.isEmpty()) { System.out.print(stack.pop() + " "); } } private void dfs(Graph graph, int v) { graph.setVisited(v, true); for (int adjVertex : graph.getAdj(v)) { if (!graph.isVisited(adjVertex)) { dfs(graph, adjVertex); } } stack.push(v); } public static void main(String[] args) { Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); TopologicalSortDFS sortDFS = new TopologicalSortDFS(); sortDFS.topologicalSort(g); } }
참고
위상 정렬(Topological sort) 개념 및 구현
목차 위상 정렬(Topological sort) 개념 및 구현 비순환 방향 그래프 (DAG: Directed Acyclic Graph) Directed Acyclic Graph (DAG)는 사이클이 없는 방향 그래프입니다. DAG는 이벤트 간의 우선순위를 나타내기 위해 주
yoongrammer.tistory.com
예시 문제: https://www.acmicpc.net/problem/1005
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.ArrayDeque; import java.util.ArrayList; import java.util.Queue; import java.util.StringTokenizer; public class _1005 { public static boolean[] visited; public static int N; public static int sum; public static int total; public static int[] buildTime; public static ArrayList<Integer>[] graph; public static int[] in_degree; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); int T = Integer.parseInt(br.readLine()); for (int i = 0; i < T; i++) { StringTokenizer st = new StringTokenizer(br.readLine()); N = Integer.parseInt(st.nextToken()); //건물 개수 int K = Integer.parseInt(st.nextToken()); //규칙 개수 buildTime = new int[N + 1];//건물 짓느데 걸리는 시간 st = new StringTokenizer(br.readLine()); for (int j = 1; j <= N; j++) { buildTime[j] = Integer.parseInt(st.nextToken()); } graph = new ArrayList[N + 1]; for (int k = 0; k <= N; k++) { graph[k] = new ArrayList<>(); } for (int k = 0; k < K; k++) { st = new StringTokenizer(br.readLine()); int start = Integer.parseInt(st.nextToken()); int end = Integer.parseInt(st.nextToken()); graph[start].add(end); } in_degree = new int[N + 1]; for (int j = 0; j <= N; j++) { if (!graph[j].isEmpty()) { for (int k : graph[j]) { in_degree[k]++; } } } int obj = Integer.parseInt(br.readLine()); System.out.println(topoSort(obj)); } } public static int topoSort(int obj) { int[] time = new int[N + 1]; Queue<Integer> curIdx = new ArrayDeque<>(); for (int i = 1; i <= N; i++) { time[i] = buildTime[i]; if (in_degree[i] == 0) { curIdx.add(i); } } while (!curIdx.isEmpty()) { int idx = curIdx.poll(); for (int i : graph[idx]) { time[i] = Math.max(time[i], time[idx] + buildTime[i]); in_degree[i]--; if(in_degree[i]==0) curIdx.add(i); } } return time[obj]; } }
예시 문제: https://www.acmicpc.net/problem/14567
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.ArrayList; import java.util.Arrays; import java.util.StringTokenizer; public class _14567 { public static void main(String[] args)throws IOException { BufferedReader br=new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st=new StringTokenizer(br.readLine()); int N=Integer.parseInt(st.nextToken()); int M=Integer.parseInt(st.nextToken()); int[] in_degree=new int[N+1]; Arrays.fill(in_degree, 1); ArrayList<Integer>[] graph=new ArrayList[N+1]; for(int i=0;i<=N;i++){ graph[i]=new ArrayList<>(); } for(int i=0;i<M;i++){ st=new StringTokenizer(br.readLine()); int start=Integer.parseInt(st.nextToken()); int end=Integer.parseInt(st.nextToken()); graph[start].add(end); } for(int i=1;i<=N;i++){ if(!graph[i].isEmpty()){ for(int j:graph[i]){ in_degree[j]=Math.max(in_degree[j], in_degree[i]+1); } } } for(int i=1;i<=N;i++){ System.out.print(in_degree[i]+" "); } } }
예시 문제: https://www.acmicpc.net/problem/1766
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.ArrayList; import java.util.Collections; import java.util.PriorityQueue; import java.util.StringTokenizer; public class _1766 { static ArrayList<Integer>[] graph; static ArrayList<Integer> answer; static int[] in_degree; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); int N = Integer.parseInt(st.nextToken()); int M = Integer.parseInt(st.nextToken()); in_degree = new int[N + 1]; graph = new ArrayList[N + 1]; for (int i = 0; i <= N; i++) { graph[i] = new ArrayList<>(); } for (int i = 0; i < M; i++) { st = new StringTokenizer(br.readLine()); int start = Integer.parseInt(st.nextToken()); int end = Integer.parseInt(st.nextToken()); in_degree[end] += 1; graph[start].add(end); } for (int i = 0; i <= N; i++) { Collections.sort(graph[i]); } answer = new ArrayList<>(); PriorityQueue<Integer> pq = new PriorityQueue<>(); for (int i = 1; i <= N; i++) { if(in_degree[i]==0) pq.add(i); } while(!pq.isEmpty()){ Integer idx=pq.poll(); answer.add(idx); for(int next:graph[idx]){ if(--in_degree[next]==0){ pq.add(next); } } } for(int i:answer){ System.out.print(i+" "); } } }
'CS > Algorithm' 카테고리의 다른 글
| [LIS] 최장 증가 부분 수열 (0) | 2024.08.01 |
|---|---|
| Union-Find 연산에서 find함수 return할 때 주의할 점 (1) | 2024.07.24 |
| [MST] 프림 알고리즘 (Prim) (0) | 2024.07.22 |
| [MST] 크루스칼 알고리즘 (Kruskal) (0) | 2024.07.22 |
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
