Spanning Tree이란?

신장 트리는 그래프 내의 모든 정점을 포함하는 트리이다.
- 모든 정점들이 연결 되어 있어야 한다.
- 사이클을 포함해서는 안된다.
- 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결한다.
MST(=Minimum Spanning Tree)이란?
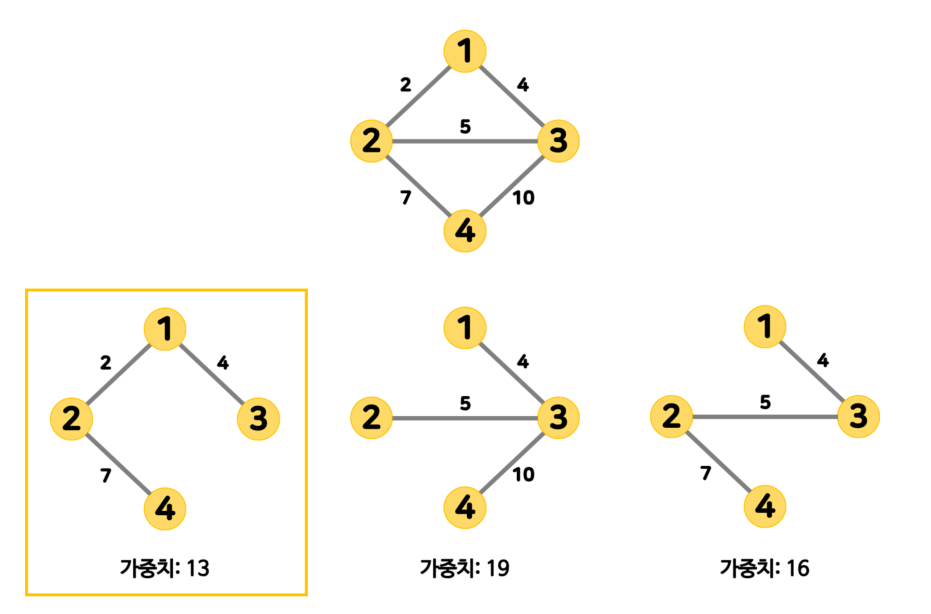
최소 신장 트리는 Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리이다.
- 간선의 가중치의 합이 최소여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
- 사이클이 포함되어서는 안된다.
MST 알고리즘 구현 방법
- 크루스칼 알고리즘 Kruskal Algorithm
- 프림 알고리즘 Prim Algorithm
크루스칼 알고리즘이란?
간선을 가중치가 작은 순서대로 그래프에 포함시킨다. (그리디 알고리즘 이용) 모든 노드를 거리가 짧은 순서대로 연결시켜야 하기 때문에 가중치를 오름차순으로 정렬한 뒤에 가중치가 작은 간선부터 그래프에 포함시킨다. 이 방법을 사용하면 가장 작은 비용으로 모든 노드를 연결한 그래프가 된다. O(Elog V)의 시간복잡도를 가진다.
주의점!
최소 신장 트리는 사이클이 발생하면 안된다.
따라서 문제에서 사이클 발생여부가 안나와있으면 Union-Find를 적용해 사이클이 발생하는지 점검한다.
구현 방법
- 주어진 그래프의 모든 간선에 대해서, 간선의 가중치를 오름차순 정렬한다.
- 정렬된 간선 순서대로 선택하기 전에 사이클 여부를 확인한다.
- 간선의 양 끝 정점을 Union 한다.
- 두 정점이 같은 집합에 속해있다면 사이클(cycle)이 있다고 판단하고 포함시키지 않는다.
(유니온 파인드 알고리즘)
예시
아래와 같이 초기화를 해준다.

1) (v, w, cost) = (1, 3, 3)
- find(1) = 1, find(3) = 3
부모 노드가 다르므로 이 간선을 MST에 추가했을 때 사이클이 생기지 않는다. 따라서 이 간선을 MST에 추가한다.
정점 1과 정점 3을 union(1, 3)을 수행하여 같은 MST에 속해있도록 한다.

2) (1, 4, 8)
- find(1) = 1, find(4) = 4
위와 동일한 이유로 간선을 추가한다.
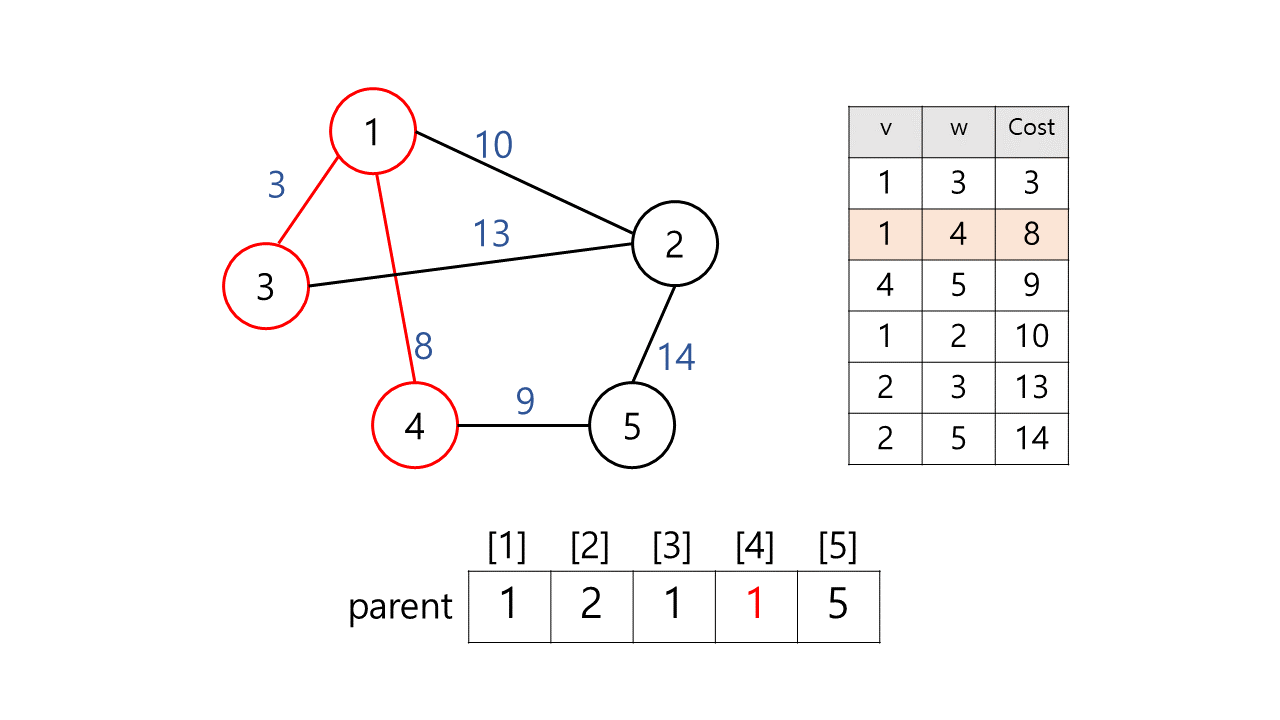
3) (4, 5, 9)
- find(4) = 1, find(5) = 5

4) (1, 2, 10)
- find(1) = 1, find(2) = 2

5) (2, 3, 13)
- find(2) = 1, find(3) = 1
두 정점의 부모 노드가 같다. 이 간선을 MST에 추가할 경우 사이클이 생기므로 추가하지 않는다.

6) (2, 5, 14)
- find(2) = 1, find(5) = 1
위와 동일한 이유로 추가하지 않는다.

모든 간선을 살피고 남은 MST의 모습이다. 이 MST의 가중치의 총 합은 30이다.

코드
public class Main {
// 유니온
public static void union(int[] parent, int x, int y) {
x = find(parent, x);
y = find(parent, y);
if(x < y) parent[y] = x;
else parent[x] = y;
}
// 파인드
public static int find(int[] parent, int x) {
if(parent[x] == x) return x;
else return find(parent, parent[x]);
}
// 크루스칼
public static void kruskal(int[][] graph, int[] parent) {
int cost = 0;
for(int i = 0; i < graph.length;i++) {
if (find(parent, graph[i][0]) != find(parent, graph[i][1])) {
cost += graph[i][2];
union(parent, graph[i][0], graph[i][1]);
}
}
// 최소 신장 트리의 총 가중치 출력
System.out.println(cost);
}
public static void main(String[] args) throws IOException {
// 간선 입력 받기, 그래프에 저장
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(bf.readLine());
int m = Integer.parseInt(bf.readLine());
int[][] graph = new int[m][3];
StringTokenizer st;
for (int i = 0; i < m; i++) {
st = new StringTokenizer(bf.readLine());
graph[i][0] = Integer.parseInt(st.nextToken()); // 간선 나가는 정점
graph[i][1] = Integer.parseInt(st.nextToken()); // 간선 들어오는 정점
graph[i][2] = Integer.parseInt(st.nextToken()); // 가중치
}
// 간선 정렬
Arrays.sort(graph, (o1, o2) -> o1[2] - o2[2]);
// 부모노드 초기화
int[] parent = new int[n + 1];
for (int i = 0; i < parent.length; i++) {
parent[i] = i;
}
//크루스칼 알고리즘 수행
kruskal(graph, parent);
}
}입력
5
6
1 3 3
1 4 8
4 5 9
1 2 10
2 3 13
2 5 14
출력 결과
30
예시 문제: https://www.acmicpc.net/problem/1197
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class _1197 {
static int[] parent;
public static int find(int x){
if(parent[x]==x)
return x;
else return find(parent[x]);
}
public static void union(int x, int y){
x=find(x);
y=find(y);
if(x!=y)
parent[y]=x;
}
public static void kruskal(int[][] graph){
int cost=0;
for(int i=0;i<graph.length;i++){
if(find(graph[i][0])!=find(graph[i][1])){
cost+=graph[i][2];
union(graph[i][0], graph[i][1]);
}
}
System.out.println(cost);
}
public static void main(String[] args)throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
int v=Integer.parseInt(st.nextToken());
int e=Integer.parseInt(st.nextToken());
int[][] map=new int[e][3];
for(int i=0;i<e;i++){
st=new StringTokenizer(br.readLine());
for(int j=0;j<3;j++){
map[i][j]=Integer.parseInt(st.nextToken()); //0: 시작 정점, 1: 종료 정점, 2: 가중치
}
}
//우선 가중치를 기준으로 오름차순 정렬해준다.
Arrays.sort(map, ((o1, o2) -> o1[2]-o2[2]));
parent=new int[v+1];
for(int i=0;i<=v;i++){
parent[i]=i;
}
kruskal(map);
}
}'CS > Algorithm' 카테고리의 다른 글
| [그래프] 위상 정렬 (Topological Sorting) 알고리즘 (0) | 2024.07.23 |
|---|---|
| [MST] 프림 알고리즘 (Prim) (0) | 2024.07.22 |
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
| [최단거리] 플로이드-워셜 알고리즘 (Floyd-Warshal) (0) | 2024.07.11 |
| [최단거리] 벨만-포드 알고리즘 (Bellman-Ford) (2) | 2024.07.10 |
Spanning Tree이란?

신장 트리는 그래프 내의 모든 정점을 포함하는 트리이다.
- 모든 정점들이 연결 되어 있어야 한다.
- 사이클을 포함해서는 안된다.
- 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결한다.
MST(=Minimum Spanning Tree)이란?

최소 신장 트리는 Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리이다.
- 간선의 가중치의 합이 최소여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
- 사이클이 포함되어서는 안된다.
MST 알고리즘 구현 방법
- 크루스칼 알고리즘 Kruskal Algorithm
- 프림 알고리즘 Prim Algorithm
크루스칼 알고리즘이란?
간선을 가중치가 작은 순서대로 그래프에 포함시킨다. (그리디 알고리즘 이용) 모든 노드를 거리가 짧은 순서대로 연결시켜야 하기 때문에 가중치를 오름차순으로 정렬한 뒤에 가중치가 작은 간선부터 그래프에 포함시킨다. 이 방법을 사용하면 가장 작은 비용으로 모든 노드를 연결한 그래프가 된다. O(Elog V)의 시간복잡도를 가진다.
주의점!
최소 신장 트리는 사이클이 발생하면 안된다.
따라서 문제에서 사이클 발생여부가 안나와있으면 Union-Find를 적용해 사이클이 발생하는지 점검한다.
구현 방법
- 주어진 그래프의 모든 간선에 대해서, 간선의 가중치를 오름차순 정렬한다.
- 정렬된 간선 순서대로 선택하기 전에 사이클 여부를 확인한다.
- 간선의 양 끝 정점을 Union 한다.
- 두 정점이 같은 집합에 속해있다면 사이클(cycle)이 있다고 판단하고 포함시키지 않는다.
(유니온 파인드 알고리즘)
예시
아래와 같이 초기화를 해준다.

1) (v, w, cost) = (1, 3, 3)
- find(1) = 1, find(3) = 3
부모 노드가 다르므로 이 간선을 MST에 추가했을 때 사이클이 생기지 않는다. 따라서 이 간선을 MST에 추가한다.
정점 1과 정점 3을 union(1, 3)을 수행하여 같은 MST에 속해있도록 한다.

2) (1, 4, 8)
- find(1) = 1, find(4) = 4
위와 동일한 이유로 간선을 추가한다.

3) (4, 5, 9)
- find(4) = 1, find(5) = 5

4) (1, 2, 10)
- find(1) = 1, find(2) = 2

5) (2, 3, 13)
- find(2) = 1, find(3) = 1
두 정점의 부모 노드가 같다. 이 간선을 MST에 추가할 경우 사이클이 생기므로 추가하지 않는다.

6) (2, 5, 14)
- find(2) = 1, find(5) = 1
위와 동일한 이유로 추가하지 않는다.

모든 간선을 살피고 남은 MST의 모습이다. 이 MST의 가중치의 총 합은 30이다.

코드
public class Main { // 유니온 public static void union(int[] parent, int x, int y) { x = find(parent, x); y = find(parent, y); if(x < y) parent[y] = x; else parent[x] = y; } // 파인드 public static int find(int[] parent, int x) { if(parent[x] == x) return x; else return find(parent, parent[x]); } // 크루스칼 public static void kruskal(int[][] graph, int[] parent) { int cost = 0; for(int i = 0; i < graph.length;i++) { if (find(parent, graph[i][0]) != find(parent, graph[i][1])) { cost += graph[i][2]; union(parent, graph[i][0], graph[i][1]); } } // 최소 신장 트리의 총 가중치 출력 System.out.println(cost); } public static void main(String[] args) throws IOException { // 간선 입력 받기, 그래프에 저장 BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); int n = Integer.parseInt(bf.readLine()); int m = Integer.parseInt(bf.readLine()); int[][] graph = new int[m][3]; StringTokenizer st; for (int i = 0; i < m; i++) { st = new StringTokenizer(bf.readLine()); graph[i][0] = Integer.parseInt(st.nextToken()); // 간선 나가는 정점 graph[i][1] = Integer.parseInt(st.nextToken()); // 간선 들어오는 정점 graph[i][2] = Integer.parseInt(st.nextToken()); // 가중치 } // 간선 정렬 Arrays.sort(graph, (o1, o2) -> o1[2] - o2[2]); // 부모노드 초기화 int[] parent = new int[n + 1]; for (int i = 0; i < parent.length; i++) { parent[i] = i; } //크루스칼 알고리즘 수행 kruskal(graph, parent); } }
입력 5 6 1 3 3 1 4 8 4 5 9 1 2 10 2 3 13 2 5 14 출력 결과 30
예시 문제: https://www.acmicpc.net/problem/1197
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.Arrays; import java.util.StringTokenizer; public class _1197 { static int[] parent; public static int find(int x){ if(parent[x]==x) return x; else return find(parent[x]); } public static void union(int x, int y){ x=find(x); y=find(y); if(x!=y) parent[y]=x; } public static void kruskal(int[][] graph){ int cost=0; for(int i=0;i<graph.length;i++){ if(find(graph[i][0])!=find(graph[i][1])){ cost+=graph[i][2]; union(graph[i][0], graph[i][1]); } } System.out.println(cost); } public static void main(String[] args)throws IOException { BufferedReader br=new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st=new StringTokenizer(br.readLine()); int v=Integer.parseInt(st.nextToken()); int e=Integer.parseInt(st.nextToken()); int[][] map=new int[e][3]; for(int i=0;i<e;i++){ st=new StringTokenizer(br.readLine()); for(int j=0;j<3;j++){ map[i][j]=Integer.parseInt(st.nextToken()); //0: 시작 정점, 1: 종료 정점, 2: 가중치 } } //우선 가중치를 기준으로 오름차순 정렬해준다. Arrays.sort(map, ((o1, o2) -> o1[2]-o2[2])); parent=new int[v+1]; for(int i=0;i<=v;i++){ parent[i]=i; } kruskal(map); } }
'CS > Algorithm' 카테고리의 다른 글
| [그래프] 위상 정렬 (Topological Sorting) 알고리즘 (0) | 2024.07.23 |
|---|---|
| [MST] 프림 알고리즘 (Prim) (0) | 2024.07.22 |
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
| [최단거리] 플로이드-워셜 알고리즘 (Floyd-Warshal) (0) | 2024.07.11 |
| [최단거리] 벨만-포드 알고리즘 (Bellman-Ford) (2) | 2024.07.10 |
