벨만-포드 알고리즘이란?
벨만-포드 알고리즘은 다익스트라 알고리즘과 마찬가지로 한 정점에서 다른 모든 정점까지의 최단 경로를 구하는 알고리즘이다. 이때, 다익스트라와 달리 간선의 가중치가 음수인 경우에도 최단 거리를 구할 수 있다. 음의 사이클이 없고 한 노드에서 다른 노드까지의 최단 경로를 많아봐야 V-1개의 간선을 지난다는 가정에서 시작된다. 다익스트라 알고리즘에 비해 효율이 떨어지지만 더 많은 그래프에 대해서 정확한 답을 구할 수 있다.
| 다익스트라 | 벨만-포드 | |
| 음수 가중치 | X | O |
| 음수 사이클 | X | X |
| 시간복잡도 | O(mlog n) | O(mn) |
❗️벨만-포드가 가중치가 음수인 경우에도 최단 거리를 구할 수 있는 이유
다익스트라 알고리즘에서는 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택해서 1단계씩 최단 거리를 구해간다. 하지만 벨만-포드 알고리즘에서는, 매 단계마다 모든 간선을 전부 확인하면서 모든 노드 간의 최단 거리를 구해간다. 따라서 다익스트라 알고리즘은 음의 가중치를 가질 수 없고, 벨만-포드는 음의 가중치를 가질 수 있는 것이다.
구현 방법
- 출발 노드를 설정하고, 최단 거리 테이블을 초기화한다.
- 다음의 과정을 (V(=정점개수) - 1)번 반복한다.
- 모든 간선 E개를 하나씩 확인한다.
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 이때, 한 간선에 대해 dist 값이 INF가 아닌 정점이 연결된 경우에만 해당 간선을 탐색하여야 한다
❗️만약 음의 사이클이 발생하는지 체크하고 싶다면 2번 과정을 한 번 더 수행한다.
➡️ 이때 최단 거리 테이블이 갱신된다면 음의 사이클이 존재하는 것이다.
예시
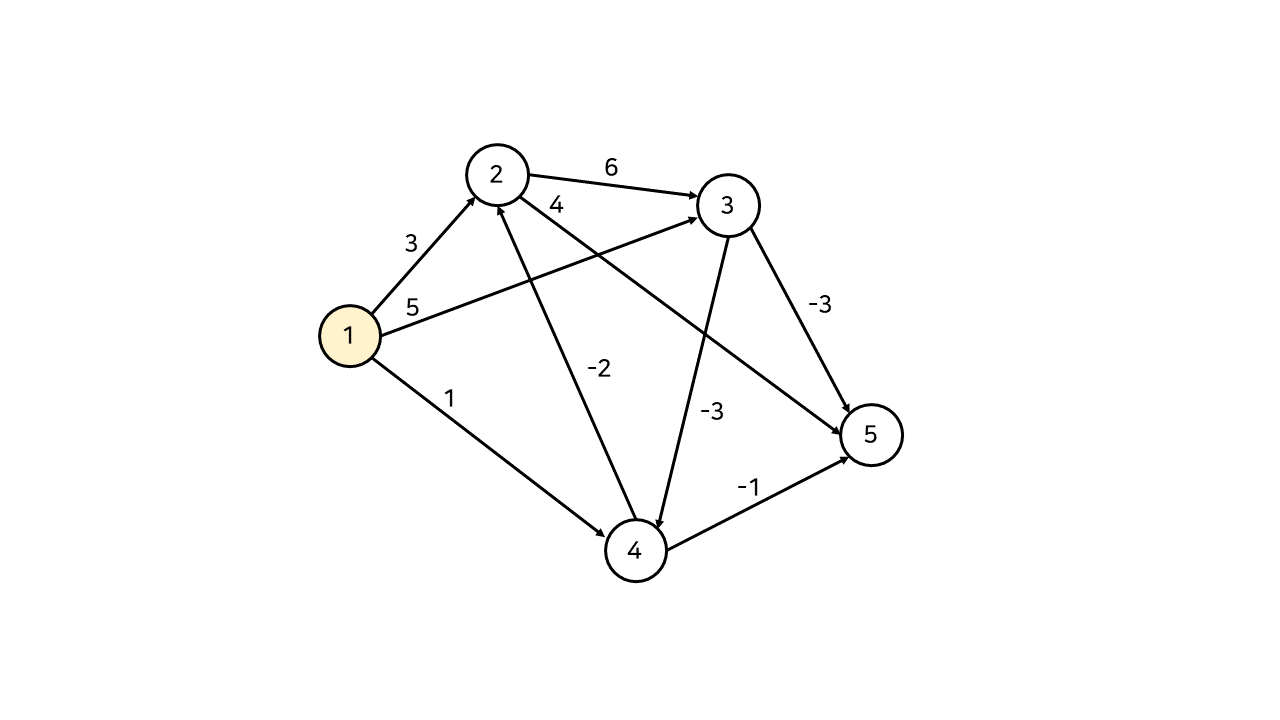
다음과 같은 음의 가중치가 포함된 그래프에서, 1번 노드에서 출발하여 각 모든 노드에 대해 최단경로를 구해보자.
[Iteration 1]
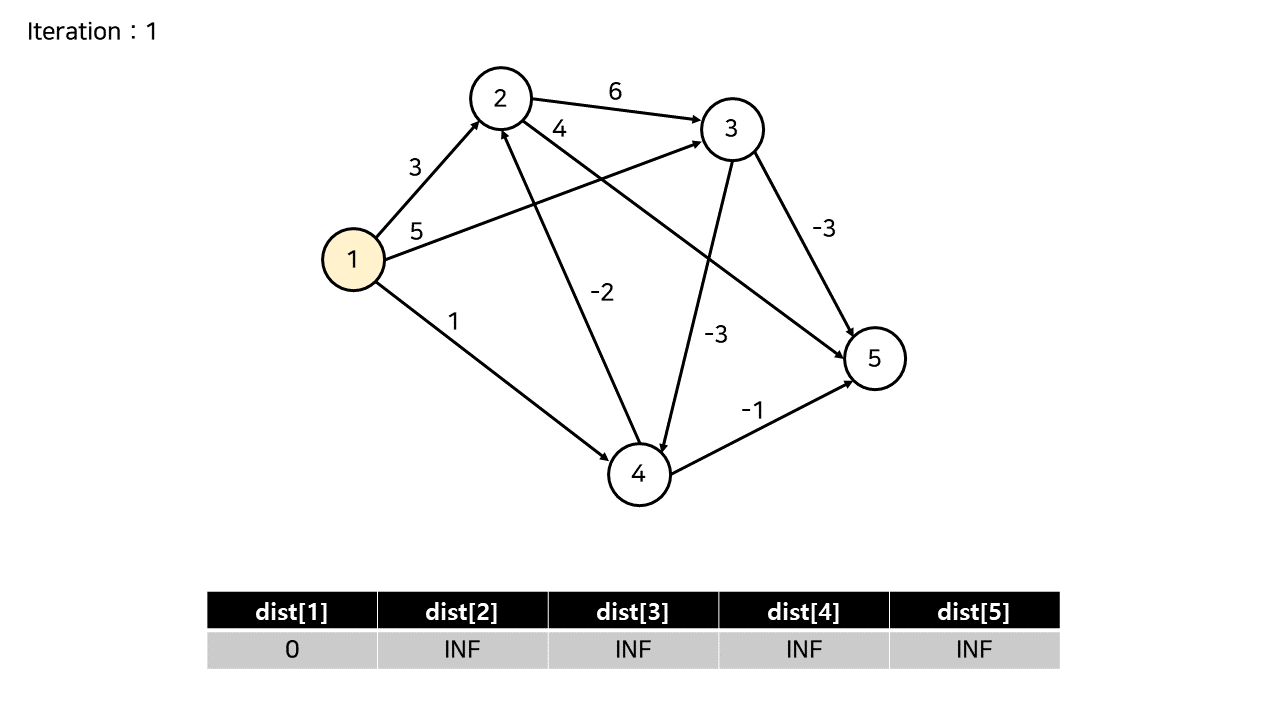
처음 iteration은 출발 노드인 1번 노드에 대해 시작한다.
각 간선을 탐색하는 순서는 상관이 없으나, 한 간선에 대해 dist 값이 INF가 아닌 정점이 연결된 경우에만
해당 간선을 탐색하여야 한다. (즉, 도달할 수 있는 정점이 연결된 간선에 대해서만 탐색)
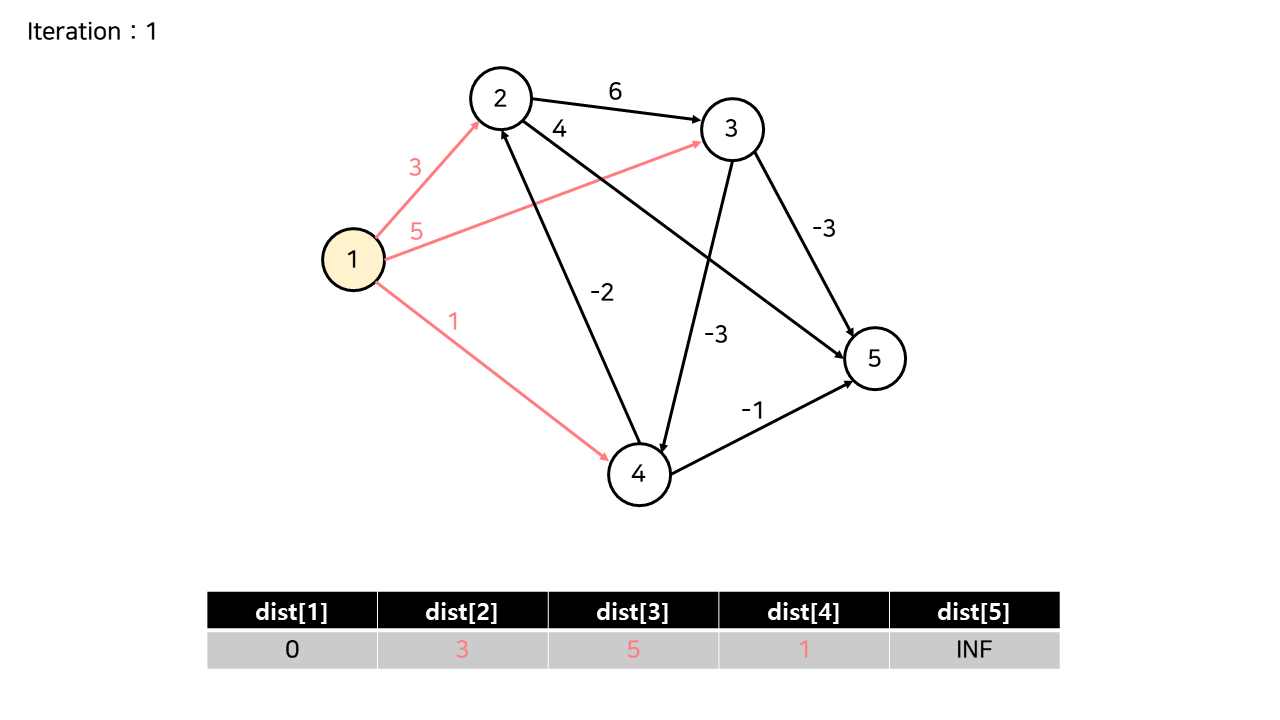
1번 노드에서 나가는 3개의 간선에 의해 dist[2], dist[3], dist[4]가 갱신되었다.
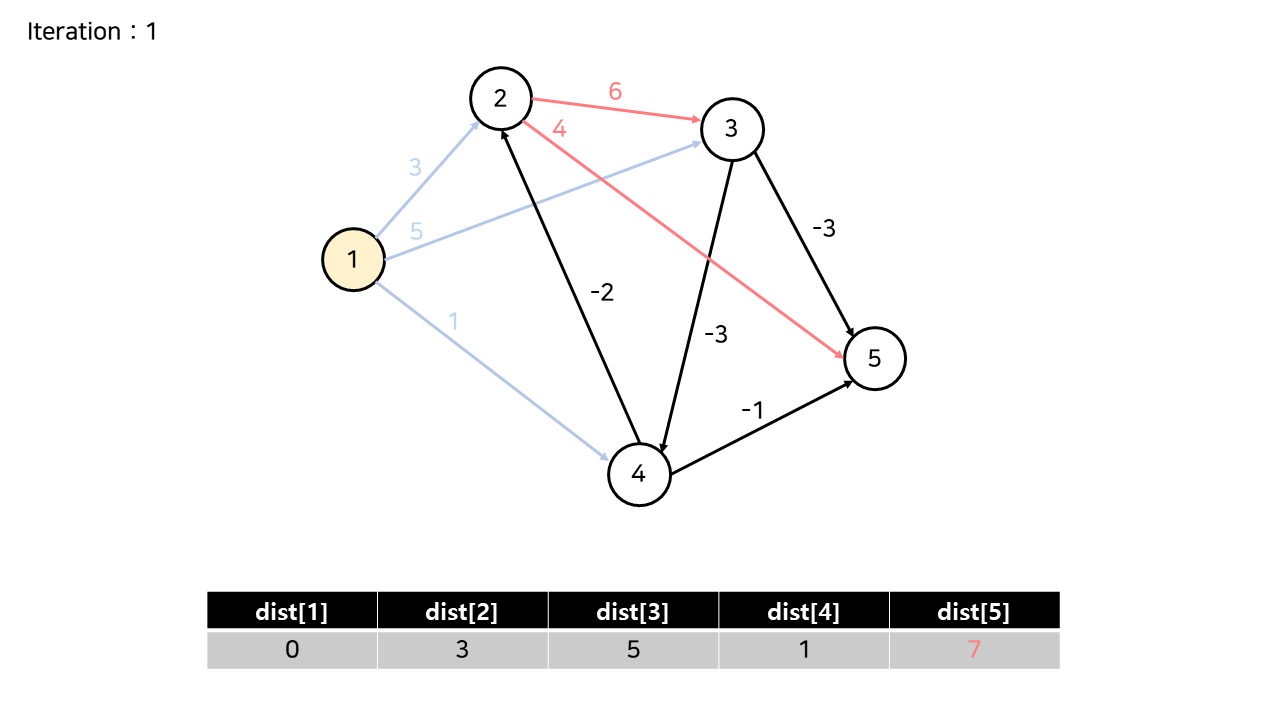
2번 노드에서 나가는 간선에 의해 dist[5]가 7로 갱신되었다.

3번 노드에서 나가는 간선들에 의해 dist[5]가 6으로 갱신되었다. (3 + 6 - 3)
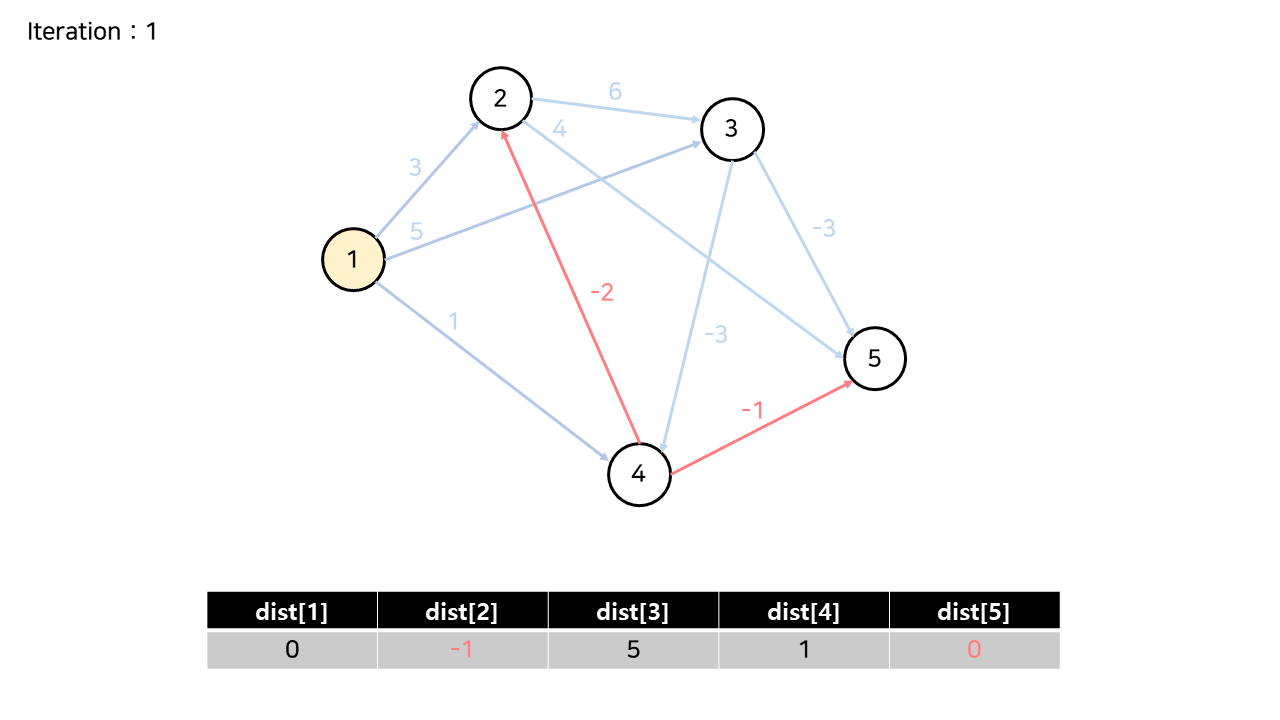
4번 노드에서 나가는 간선들에 의해, dist[2]와 dist[5]가 갱신되었다.
[Iteration 2]
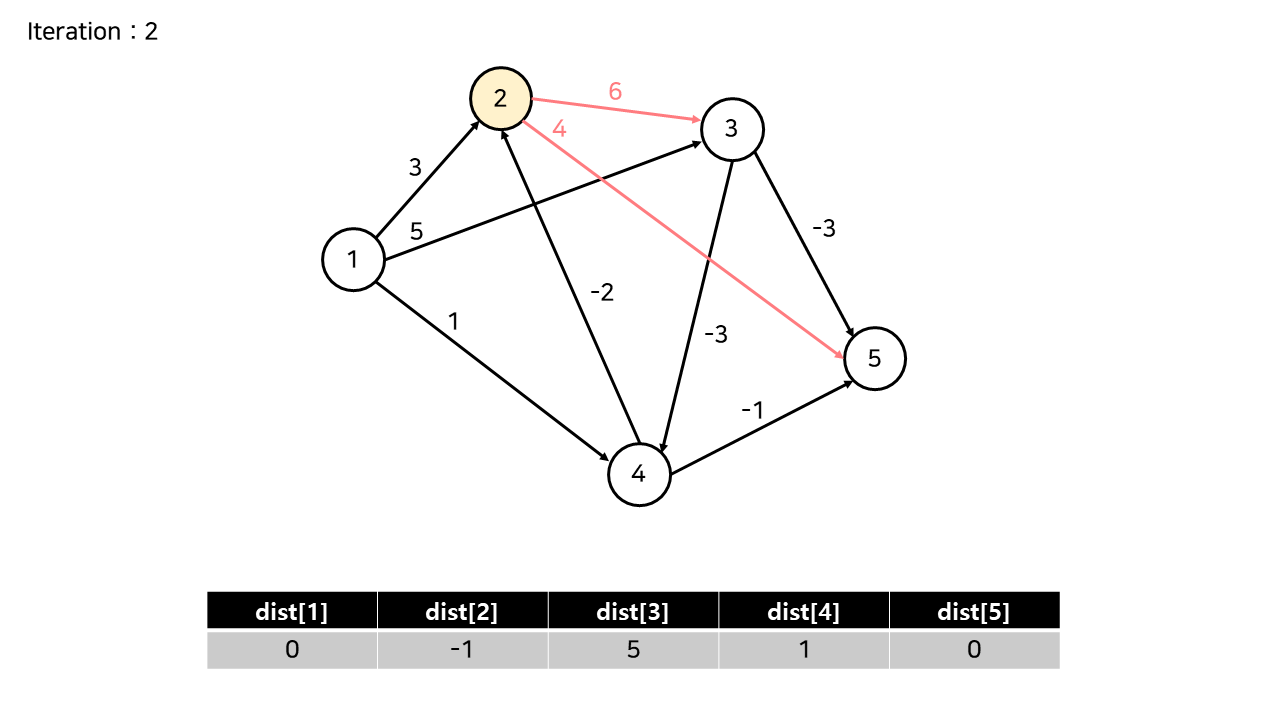

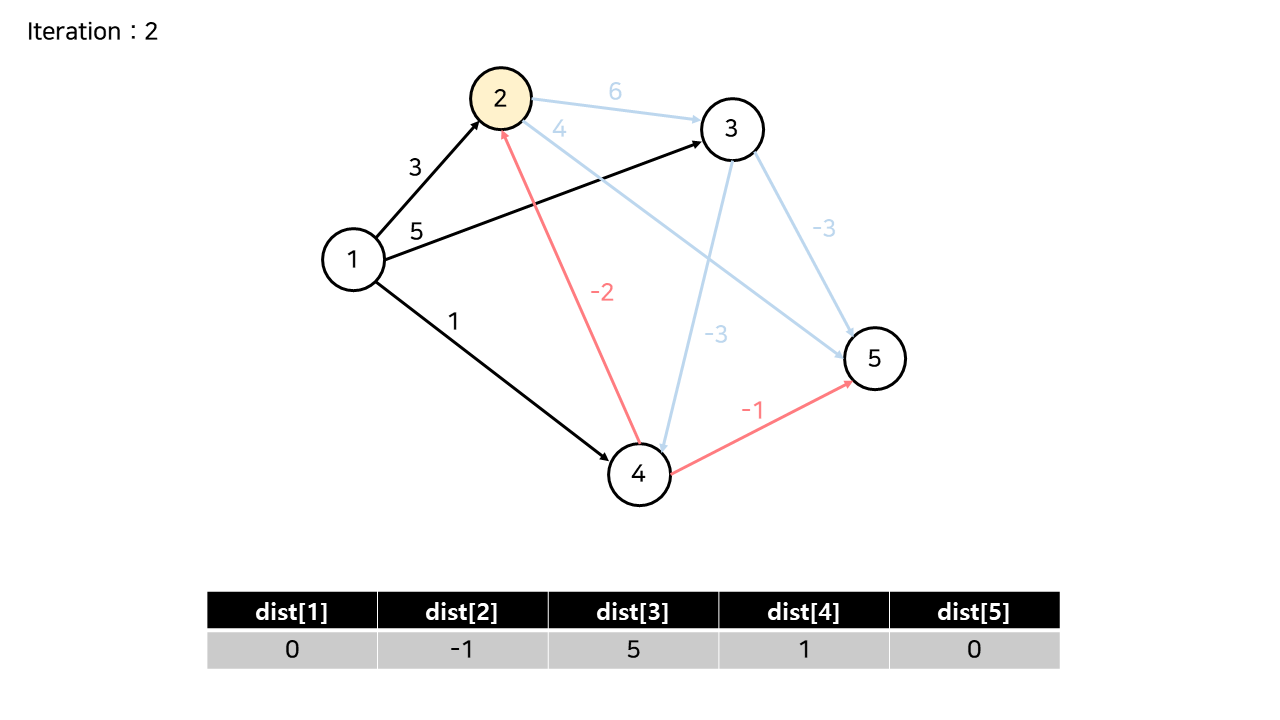

이후의 Iteration에서는, 다른 노드를 순서대로 시작점으로 두고 최단거리를 갱신한다.
(이 예제에서는 더 이상 갱신이 발생하지 않는다.)
이때, (정점의 개수 -1 )번 동안 최단거리 초기화 작업을 수행할 때 더 이상 최단거리 초기화 작업이 이루어지지 않으면 반복문을 종료한다.
음의 사이클
벨만-포드의 알고리즘은 음의 사이클이 없다는 가정 하에 출발하였다. 음의 사이클은 그래프의 존재하는 사이클의 가중치 합이 음수인 경우를 말한다.

빨간색으로 칠해진 2-3-4 사이클은 음의 사이클이다. 이 사이클을 한 바퀴 돌 때마다, 가중치 합이 음수(3 - 2 - 2 = -1)가 되므로 2-3-4 사이클을 반복할수록 경로의 거리가 작아진다. 벨만-포드 알고리즘은 한 정점으로부터 다른 정점까지의 최단경로는 많아봐야 V-1개의 간선을 지난다는 가정 하에 출발했지만, 위와 같은 음의 사이클이 존재한다면 간선을 V-1개 초과하여 지날수록 더욱 짧은 거리의 경로를 확인할 수 있게 된다. 즉, 최단 경로가 V-1개보다 많은 간선을 지나게 된다면 음의 사이클이 존재한다는 의미이다. 음의 사이클이 존재하면 최단경로를 구할 수 없다.
음의 사이클이 존재하는지 확인하는 방법
벨만-포드 알고리즘의 V - 1번까지의 Iteration 이후 더 많은 Iteration을 돌리는 것이다. V-1까지 계속 최단거리 업데이트가 발생했을 경우 V번도 업데이트가 발생하면 음수 사이클이 일어났다고 판단한다. 따라서, 최소 V번의 Iteration을 통해 벨만-포드 알고리즘은 음의 사이클의 존재 여부도 파악할 수 있다.
예시 문제
https://www.acmicpc.net/problem/11657
import java.util.*;
import java.io.*;
public class _11657 {
public static class Edge {
public int start;
public int end;
public int distance;
public Edge(int start, int end, int distance){
this.start=start;
this.end=end;
this.distance=distance;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
int V=Integer.parseInt(st.nextToken()); //
int E=Integer.parseInt(st.nextToken());
long[] distArr=new long[V+1];
long INF= Long.MAX_VALUE;
Arrays.fill(distArr, INF);
distArr[1]=0;
ArrayList<Edge> graph=new ArrayList<>();
for(int i=0;i<E;i++){
st=new StringTokenizer(br.readLine());
int start=Integer.parseInt(st.nextToken());
int end=Integer.parseInt(st.nextToken());
int distance=Integer.parseInt(st.nextToken());
graph.add(new Edge(start,end,distance));
}
for(int i=1;i<=V;i++){
for(int j=0;j<E;j++){
Edge edge=graph.get(j);
if(distArr[edge.start]!=INF&&distArr[edge.end]>distArr[edge.start]+edge.distance){
distArr[edge.end]=distArr[edge.start]+edge.distance;
}
}
}
//음의 사이클 확인
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
for(int i=1;i<=V;i++){
for(int j=0;j<E;j++){
Edge edge=graph.get(j);
if(distArr[edge.start]!=INF&&distArr[edge.end]>distArr[edge.start]+edge.distance){
bw.write("-1\n");
bw.flush();
bw.close();
return;
}
}
}
for(int i=2;i<=V;i++){
if(distArr[i]!=INF)
bw.write(distArr[i]+"\n");
else
bw.write("-1\n");
bw.flush();
}
bw.close();
}
}
예시 문제 2: https://www.acmicpc.net/problem/1865
- 모든 정점을 출발점으로 조사해서 음의 사이클이 발생하는지 확인
- 이때, 더 이상 최단거리 초기화가 일어나지 않았을 경우 반복문을 종료하고, (정점의 개수 - 1)번까지 계속 업데이트가 발생했을 경우에 음수 사이클을 체크해준다 <- 이걸 하지 않으면 시간초과가 일어남.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class _1865 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int T = Integer.parseInt(st.nextToken());
for (int i = 0; i < T; i++) {
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int W = Integer.parseInt(st.nextToken());
ArrayList<Edge> graph = new ArrayList<>();
for (int j = 0; j < M; j++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int t = Integer.parseInt(st.nextToken());
graph.add(new Edge(s, e, t));
graph.add(new Edge(e, s, t));
}
for (int j = 0; j < W; j++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int t = Integer.parseInt(st.nextToken());
graph.add(new Edge(s, e, -t));
}
boolean flag = false;
for (int s = 1; s <= N; s++) {
if (bellmanFord(s, graph, N)) {
flag = true;
break;
}
}
if (flag)
System.out.println("YES");
else
System.out.println("NO");
}
}
public static boolean bellmanFord(int start, ArrayList<Edge> graph, int N) {
long[] dist = new long[N + 1];
long INF = Long.MAX_VALUE;
Arrays.fill(dist, INF);
dist[start] = 0;
int m = graph.size();
boolean update = false;
for (int i = 0; i < N; i++) {
update = false;
for (int j = 0; j < m; j++) {
Edge edge = graph.get(j);
if (dist[edge.start] != INF && dist[edge.end] > dist[edge.start] + edge.val) {
dist[edge.end] = dist[edge.start] + edge.val;
update = true;
}
}
if (!update)
break;
}
if (update) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < m; j++) {
Edge edge = graph.get(j);
if (dist[edge.start] != INF && dist[edge.end] > dist[edge.start] + edge.val) {
return true;
}
}
}
}
return false;
}
public static class Edge {
public int start;
public int end;
public int val;
public Edge(int start, int end, int val) {
this.start = start;
this.end = end;
this.val = val;
}
}
}'CS > Algorithm' 카테고리의 다른 글
| [MST] 크루스칼 알고리즘 (Kruskal) (0) | 2024.07.22 |
|---|---|
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
| [최단거리] 플로이드-워셜 알고리즘 (Floyd-Warshal) (0) | 2024.07.11 |
| [최단거리] 다익스트라 알고리즘 (Dijkstra) (0) | 2024.07.10 |
| [그래프 탐색] DFS (0) | 2023.02.09 |
