다익스트라 알고리즘이란?
다익스트라 알고리즘은 기본적으로 greedy와 dp를 사용한 알고리즘으로 그래프의 최단 경로를 구하는 알고리즘이다. 하나의 정점에서 출발하는 최단 거리를 구하는 것이다. 이때 간선의 가중치는 양수여야 한다. 인접 행렬로 표현된 그래프의 경우 시간 복잡도 O(n^2)이지만 우선순위 큐를 사용하면 시간 복잡도 O(mlog n)까지 낮출 수 있다.
음의 가중치를 가지면 안되는 이유
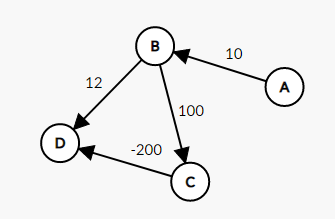
다음과 같은 경우에 다익스트라 알고리즘은 A->B->D 총 비용 22가 가장 최소 경로라고 생각 할 것이다. (A-B-D<A-B-C이므로) 하지만 A->B->C->D가 총-90 으로 값이 더 작다. 즉, 위와 같이 음의 가중치가 포함된 그래프의 최단 경로는 다익스트라 알고리즘으로 구할 수 없는 경우가 있다.
동작 과정
- 출발지에서 인접한 노드의 (거리, 노드 idx)를 우선순위 큐에 추가한다.
- 우선순위 큐에서 하나씩 꺼내 방문하지 않은 인접한 노드를 방문한다.
- visited 배열 이용
- 노드의 현재 거리가 이전에 기록된 최단 거리보다 크다면, 그 노드는 이미 최적의 경로로 처리된 것으로 간주하고 스킵
- 이때 이전 기록한 값보다 작으면(최단거리면) 갱신하고 우선순위 큐에 추가한다.
- 2-3과정을 우선순위 큐가 비어있을 때까지 (더 이상 방문할 노드가 없을 때까지) 반복한다.
예시
1) 시작 노드 설정

| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | INF | INF | INF | INF | INF | INF |
시작 노드를 충무로역이라고 하면 시작 노드 충무로역에서 충무로역까지의 거리를 0으로 하고, 이 노드를 우선순위 큐에 넣어준다.
| 우선순위 큐 (거리: 0, 노드: 충무로) |
2) 충무로
우선순위 큐에 있는 (거리: 0, 노드: 충무로) 노드를 뽑아 충무로 노드를 탐색한다.
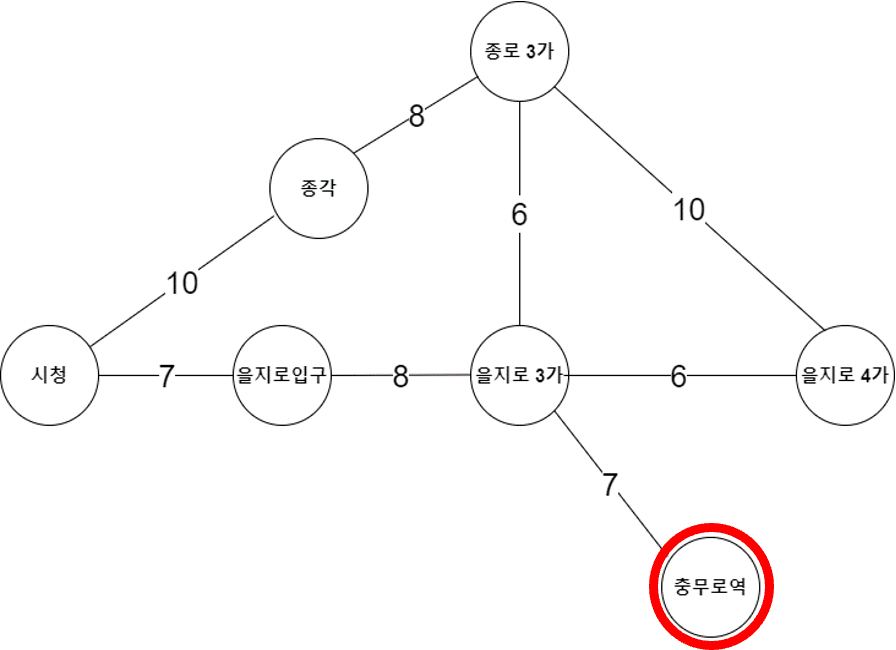
| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | INF | INF | INF | INF | INF |
충무로역에서 갈 수 있는 노드는 을지로3가역 뿐이다. 해당 노드들을 마찬가지로 우선순위 큐에 넣어준다.
| 우선순위 큐 (거리: 7, 노드: 을지로3가) |
3) 을지로 3가
우선순위 큐에 있는 (거리: 7, 노드: 을지로3가) 노드를 뽑아 을지로 3가를 탐색한다.

| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | 15 | INF | INF | 13 | 13 |
을지로3가역에서 갈 수 있는 역은 충무로, 을지로입구, 종로3가, 을지로 4가이다. 을지로 3가, 을지로입구, 종로3가역까지의 최단거리를 갱신해주고 이 노드들을 모두 우선순위 큐에 넣어준다.
| 우선순위 큐 (거리: 13, 노드: 종로3가), (거리: 13, 을지로4가), (거리: 15, 을지로입구) |
4) 종로 3가
우선순위 큐에서 가장 앞에 있는 (거리: 13, 노드: 종로3가) 노드를 뽑아 종로 3가를 탐색한다.

| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | 15 | INF | 21 | 13 | 13 |
종로 3가에서 갈 수 있는 역은 종각, 을지로 3가이다. 그 중 종각까지의 최단 거리가 갱신이 되므로 이 노드를 우선순위 큐에 넣어준다.
| 우선순위 큐 (거리: 13, 을지로4가), (거리: 15, 을지로입구) (거리:21, 종각) |
5) 을지로 4가
우선순위 큐에서 가장 앞에 있는 (거리: 13, 을지로4가) 노드를 뽑아 을지로 4가를 탐색한다.

| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | 15 | INF | 21 | 13 | 13 |
을지로 4가에서 갱신되는 최단거리는 없으므로 우선순위큐에 추가를 안 해준다.
| 우선순위 큐 (거리: 15, 을지로입구) (거리:21, 종각) |
6) 을지로 입구
우선순위 큐에서 가장 앞에 있는 (거리: 15, 을지로입구) 노드를 뽑아 을지로 입구 노드를 탐색한다.
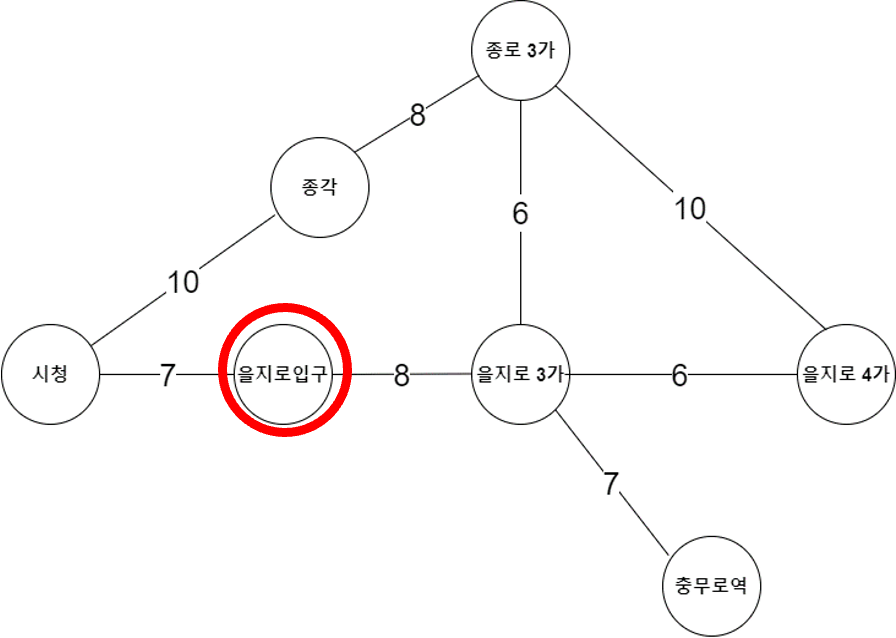
| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | 15 | 22 | 21 | 13 | 13 |
을지로 입구에서 시청까지의 최단거리가 갱신이 되므로 이 노드를 우선순위 큐에 추가한다.
| 우선순위 큐 (거리: 21, 종각) (거리: 22, 시청) |
7) 종각
우선순위 큐에서 가장 앞에 있는 (거리:-21, 종각) 노드를 뽑아 종각 노드를 탐색한다.

| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | 15 | 22 | 21 | 13 | 13 |
종각역에서 갱신되는 최단거리는 없으므로 추가를 안해준다.
| 우선순위 큐 (거리: 22, 시청) |
8) 시청
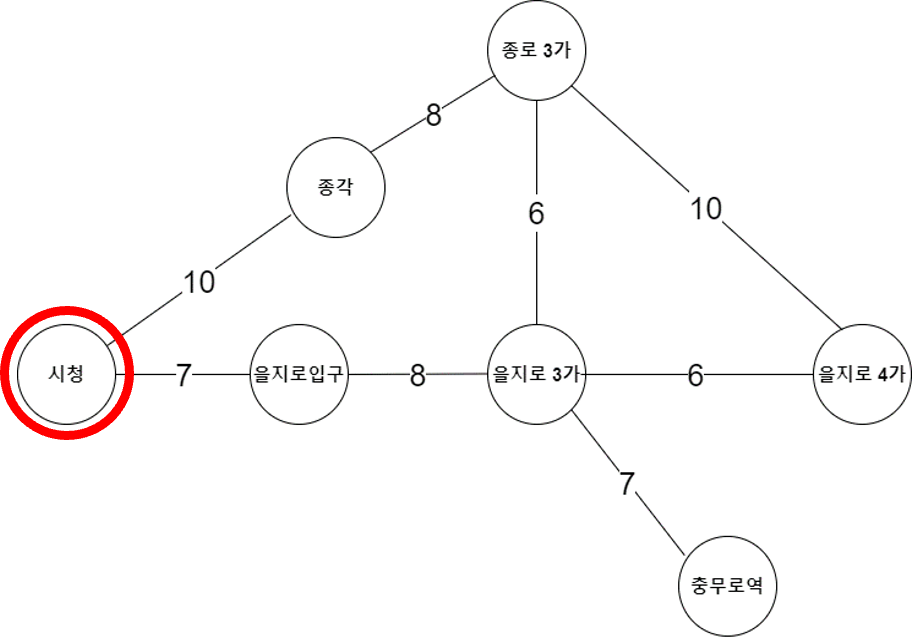
| 노드 이름 | 충무로 | 을지로3가 | 을지로입구 | 시청 | 종각 | 종로3가 | 을지로4가 |
| 거리 | 0 | 7 | 15 | 22 | 21 | 13 | 13 |
시청역에서 갱신되는 최단거리는 없다. 우선순위 큐가 비었으므로 충무로역에서 나머지 모든 역까지의 최단거리 알고리즘이 종료가 된다.
또한, 만약 우선순위 큐에서 꺼낸 데이터의 거리가 기존의 거리값보다 클 경우도 있을 수 있다. 이럴 때는 해당 노드를 탐색하지 않고 그냥 넘어간다.
| 우선순위 큐 empty |
코드
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.List;
import java.util.ArrayList;
public class DijkstraAlgorithm {
// 노드 클래스, 우선순위 큐에서 사용
public static class Node implements Comparable<Node> {
double distance; // 해당 노드까지의 거리
int station; // 역의 인덱스
public Node(double distance, int station) {
this.distance = distance;
this.station = station;
}
@Override
public int compareTo(Node other) {
return Double.compare(this.distance, other.distance);
}
}
// 다익스트라 알고리즘 구현
public static double[] dijkstra(int startStation, int N, List<List<Node>> graph) {
double[] dist = new double[N]; // 최단 거리를 저장할 배열
Arrays.fill(dist, Double.POSITIVE_INFINITY); // 모든 값을 무한대로 초기화
PriorityQueue<Node> pq = new PriorityQueue<>();
// 시작 역 초기화
dist[startStation] = 0;
pq.add(new Node(0.0, startStation));
while (!pq.isEmpty()) {
Node current = pq.poll();
if (current.distance > dist[current.station]) continue; // 이미 더 짧은 경로가 있으면 건너뛰기
// 인접 노드 탐색
for (Node neighbor : graph.get(current.station)) {
double newDist = current.distance + neighbor.distance;
if (newDist < dist[neighbor.station]) {
dist[neighbor.station] = newDist;
pq.add(new Node(newDist, neighbor.station));
}
}
}
return dist;
}
public static void main(String[] args) {
// 예제 실행
int N = 5; // 역의 개수
List<List<Node>> graph = new ArrayList<>();
for (int i = 0; i < N; i++) {
graph.add(new ArrayList<>());
}
// 엣지 예시 추가: (0->1, 2), (1->2, 3), (2->3, 4), (3->4, 2), (4->0, 7)
graph.get(0).add(new Node(2.0, 1));
graph.get(1).add(new Node(3.0, 2));
graph.get(2).add(new Node(4.0, 3));
graph.get(3).add(new Node(2.0, 4));
graph.get(4).add(new Node(7.0, 0));
double[] distances = dijkstra(0, N, graph);
System.out.println("0번 역에서 시작하여 각 역까지의 최단 거리: " + Arrays.toString(distances));
}
}
예시 문제
https://www.acmicpc.net/problem/1753
import java.util.*;
import java.io.*;
public class _1753 {
public static class Node implements Comparable<Node>{
public int idx;
public int distance;
@Override
public int compareTo(Node node){
return this.distance-node.distance;
}
public Node(int idx, int distance){
this.idx=idx;
this.distance=distance;
}
}
public static void main(String[] args)throws IOException{
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
int V=Integer.parseInt(st.nextToken());
int E=Integer.parseInt(st.nextToken());
int[] distArr=new int[V+1];
Arrays.fill(distArr,Integer.MAX_VALUE);
ArrayList<Node>[] adjacentNode=new ArrayList[V+1];
for(int i=0;i<=V;i++){
adjacentNode[i]=new ArrayList<>();
}
Arrays.fill(distArr, -1);
int startIdx=Integer.parseInt(br.readLine()); //시작 정점 번호
for(int i=0;i<E;i++){
st=new StringTokenizer(br.readLine());
int start=Integer.parseInt(st.nextToken());
int end=Integer.parseInt(st.nextToken());
int dist=Integer.parseInt(st.nextToken());
adjacentNode[start].add(new Node(end, dist));
}
PriorityQueue<Node> pq=new PriorityQueue<>();
pq.add(new Node(startIdx, 0));
distArr[startIdx]=0;
boolean[] visited=new boolean[V+1];
visited[startIdx]=true;
while(!pq.isEmpty()){
//노드 방문
Node curNode=pq.poll();
//인접 노드
for(Node node:adjacentNode[curNode.idx]){
if(!visited[node.idx])
if(distArr[node.idx]==-1||(distArr[node.idx]>(distArr[curNode.idx]+node.distance))){
distArr[node.idx]=distArr[curNode.idx]+node.distance;
pq.add(new Node(node.idx,distArr[curNode.idx]+node.distance));
}
}
}
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
for(int i=1;i<=V;i++){
if(distArr[i]==-1) {
bw.write("INF\n");
bw.flush();
}
else {
bw.write(distArr[i] + "\n");
bw.flush();
}
}
bw.flush();
bw.close();
}
}
'CS > Algorithm' 카테고리의 다른 글
| [MST] 크루스칼 알고리즘 (Kruskal) (0) | 2024.07.22 |
|---|---|
| [분리 집합] 분리집합(Disjoint Set)과 유니온-파인드(Union-Find) (0) | 2024.07.16 |
| [최단거리] 플로이드-워셜 알고리즘 (Floyd-Warshal) (0) | 2024.07.11 |
| [최단거리] 벨만-포드 알고리즘 (Bellman-Ford) (2) | 2024.07.10 |
| [그래프 탐색] DFS (0) | 2023.02.09 |
